5. Vigursvið¶

Different roads sometimes lead to the same castle.

-George R.R. Martin, A Game of Thrones

5.1. Vigursvið¶

5.1.1. Skilgreining¶

Vigursviðen: vector field.
Smelltu fyrir ítarlegri þýðingu. á ${\mathbb R}^2$ er vörpun

\[\displaystyle \mbox{${\bf F}$}(x,y)=F_1(x,y)\,\mbox{${\bf i}$}+F_2(x,y)\,\mbox{${\bf j}$}.\]

Þegar talað er um vigursvið þá hugsum við vigurinn $\mbox{${\bf F}$}(x,y)$ sem vigur í ${\mathbb R}^2$ sem hefur fótpunkt í punktinum $(x,y)$.

Vigursvið $\mbox{${\bf F}$}(x,y)=F_1(x,y)\mbox{${\bf i}$}+F_2(x,y)\mbox{${\bf j}$}$ er sagt samfellten: continuous.
Smelltu fyrir ítarlegri þýðingu. ef föllin $F_1(x,y)$ og $F_2(x,y)$ eru samfelld.

Vigursvið á ${\mathbb R}^3$ er vörpun

\[\displaystyle \mbox{${\bf F}$}(x,y,z)=F_1(x,y,z)\,\mbox{${\bf i}$}+F_2(x,y,z)\,\mbox{${\bf j}$}+F_3(x,y,z)\,\mbox{${\bf k}$}.\]

Við hugsum $\mbox{${\bf F}$}(x,y,z)$ sem vigur með $(x,y,z)$ sem fótpunkt. Skilgreiningin á því að vigursvið í ${\mathbb R}^3$ sé samfellt er eins og á samfeldni vigursvið í ${\mathbb R}^2$ .

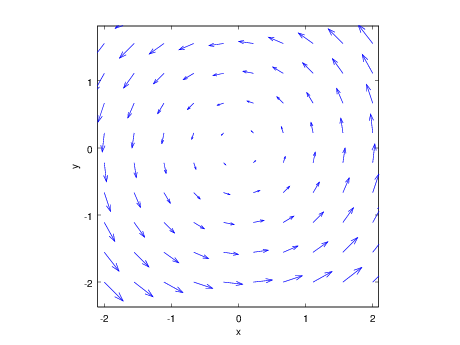
Vigursviðið $\mathbf{F}(x,y) = -y\mbox{${\bf i}$}+ x \mbox{${\bf j}$}$.

5.2. Straumlína¶

5.2.1. Skilgreining¶

Ferillen: curve.
Smelltu fyrir ítarlegri þýðingu. $C$ í planinu kallast straumlínaen: flow line.
Smelltu fyrir ítarlegri þýðingu. fyrir vigursviðen: vector field.
Smelltu fyrir ítarlegri þýðingu. $\mbox{${\bf F}$}(x,y)$ ef í hverjum punkti $(x,y)$ á ferlinum er vigurinn $\mbox{${\bf F}$}(x,y)$ snertiviguren: tangent vector.
Smelltu fyrir ítarlegri þýðingu. við ferilinn.

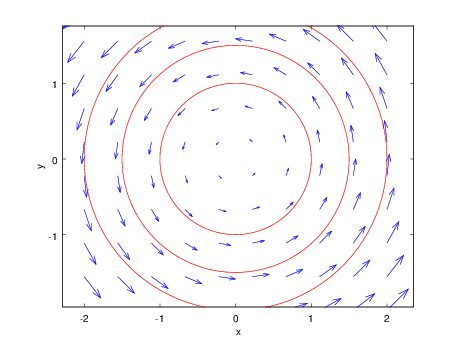
Vigursviðið $\mathbf{F}(x,y) = -y\mbox{${\bf i}$}+ x \mbox{${\bf j}$}$ ásamt nokkrum straumlínum.

5.3. Stigulsvið¶

5.3.1. Skilgreining¶

Vigursvið $\mbox{${\bf F}$}(x,y)$ kallast stigulsvið eða geymið svið (e. gradient field, conservative field) á mengi $D$ ef til er fall $\varphi(x,y)$ þannig að

\[\displaystyle \mbox{${\bf F}$}(x,y)=\nabla\varphi(x,y)\]

fyrir alla punkta $(x,y)\in D$, það er að segja ef

\[\displaystyle \mbox{${\bf F}$}(x,y)=F_1(x,y)\,\mbox{${\bf i}$}+F_2(x,y)\,\mbox{${\bf j}$}\]

þá er

\[\displaystyle F_1(x,y)=\frac{\partial}{\partial x}\varphi(x,y) \quad \text{og}\quad F_2(x,y)=\frac{\partial}{\partial y}\varphi(x,y).\]

Vigursvið $\mbox{${\bf F}$}(x,y,z)$ kallast stigulsvið eða geymið svið ef til er fall $\varphi(x,y,z)$ þannig að $\mbox{${\bf F}$}(x,y,z)=\nabla\varphi(x,y,z)$.

Fallið $\varphi$ kallast mættien: potential.
Smelltu fyrir ítarlegri þýðingu. fyrir vigursviðið $\mbox{${\bf F}$}$.

5.3.2. Setning¶

Látum $\mbox{${\bf F}$}(x,y)=F_1(x,y)\,\mbox{${\bf i}$}+F_2(x,y)\,\mbox{${\bf j}$}$ vera vigursvið þannig að föllin $F_1(x,y)$ og $F_2(x,y)$ hafi samfelldar hlutafleiður. Ef $\mbox{${\bf F}$}(x,y)$ er stigulsvið þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial}{\partial y}F_1(x,y)= \frac{\partial}{\partial x}F_2(x,y).\end{aligned}\end{align} \]

Athugasemd

Þó að hlutafleiðurnar séu jafnar þá er ekki hægt að álykta að $\mbox{${\bf F}$}$ sé stigulsvið. Þetta atriði verður rætt síðar.

5.3.3. Setning¶

Látum $\mbox{${\bf F}$}(x,y,z)=F_1(x,y,z)\,\mbox{${\bf i}$}+F_2(x,y,z)\,\mbox{${\bf j}$}+F_3(x,y,z)\,\mbox{${\bf k}$}$ vera vigursvið þannig að föllin $F_1(x,y,z), F_2(x,y,z)$ og $F_3(x,y,3)$ hafi samfelldar hlutafleiður. Ef $\mbox{${\bf F}$}(x,y,z)$ er stigulsvið þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} \frac{\partial}{\partial y}F_1(x,y,z) &= \frac{\partial}{\partial x}F_2(x,y,z), \\ \frac{\partial}{\partial z}F_1(x,y,z) &= \frac{\partial}{\partial x}F_3(x,y,z) \quad \text{og} \\ \frac{\partial}{\partial z}F_2(x,y,z)&= \frac{\partial}{\partial y}F_3(x,y,z).\end{aligned}\end{split}\end{aligned}\end{align} \]

5.3.4. Reikniaðferð¶

Finna á mættien: potential.
Smelltu fyrir ítarlegri þýðingu. $\varphi(x,y)$ fyrir stigulsvið $\mbox{${\bf F}$}(x,y)=F_1(x,y)\,\mbox{${\bf i}$}+F_2(x,y)\,\mbox{${\bf j}$}$. Viljum finna fall $\varphi(x,y)$ þannig að

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial}{\partial x}\varphi(x,y)=F_1(x,y)\qquad \mbox{og}\qquad \frac{\partial}{\partial y}\varphi(x,y)=F_2(x,y).\end{aligned}\end{align} \]

Með því að heilda þessar jöfnur fæst að

\[ \begin{align}\begin{aligned}\displaystyle \varphi(x,y)=\int F_1(x,y)\,dx+C_1(y)\\og\end{aligned}\end{align} \]

\[\displaystyle \varphi(x,y)=\int F_2(x,y)\,dy+C_2(x).\]

Þegar fyrra stofnfallið er reiknað þá er $y$ hugsað sem fasti og því fæst heildunarfasti sem getur verið fall af $y$. Lokaskrefið er svo að horfa á jöfnurnar tvær hér að ofan og sjá hvort ekki er hægt að finna gildi fyrir heildunarfastanna $C_1(x)$ og $C_2(y)$ þannig að sama formúlan fyrir $\varphi(x,y)$ fáist.

5.4. Heildi falls yfir feril¶

5.4.1. Skilgreining¶

Látum $\cal C$ vera feril í ${\mathbb R}^2$ stikaðan af samfellt diffranlegum stikaferli $\mbox{${\bf r}$}:[a,b]\rightarrow{\mathbb R}^2$. Ritum $\mbox{${\bf r}$}(t)=(x(t),y(t))$. Heildi falls $f(x,y)$ yfir ferilinn $\cal C$ með tilliti til bogalengdar er skilgreint sem

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} \int_{\cal C}f(x,y)\,ds&=\int_a^b f(\mbox{${\bf r}$}(t))\,|\mbox{${\bf r}$}'(t)|\,dt\\ &=\int_a^b f(x(t),y(t))\,\sqrt{x'(t)^2+y'(t)^2}\,dt.\end{aligned}\end{split}\end{aligned}\end{align} \]

Sama aðferð notuð til að skilgreina heildi falls yfir feril í ${\mathbb R}^3$.

5.4.2. Setning¶

Látum $\cal C$ vera feril í ${\mathbb R}^2$. Gerum ráð fyrir að $\mbox{${\bf r}$}_1$ og $\mbox{${\bf r}$}_2$ séu tveir samfellt diffranlegir stikaferlar sem báðir stika ferilinn $\cal C$. Ef fall $f(x,y)$ er heildað yfir $\cal C$ þá fæst sama útkoma hvort sem stikunin $\mbox{${\bf r}$}_1$ eða stikunin $\mbox{${\bf r}$}_2$ er notuð við útreikningana.

5.4.3. Skilgreining¶

Ferill $\cal C$ í plani er sagður samfellt diffranlegur á köflum ef til er stikun $\mbox{${\bf r}$}:[a,b]\rightarrow {\mathbb R}^2$ á $\cal C$ þannig að til eru punktar $a=t_0<t_1<t_2<\cdots<t_n<t_{n+1}=b$ þannig að á hverju bili $(t_i,t_{i+1})$ er $\mbox{${\bf r}$}$ samfellt diffranleguren: continuously differentiable.
Smelltu fyrir ítarlegri þýðingu. ferill og markgildinEkki fannst þýðing á hugtakinu: markgildi

\[ \begin{align}\begin{aligned}\displaystyle\\\lim_{t\rightarrow t_i^+}\mbox{${\bf r}$}'(t)\qquad\mbox{og}\qquad \lim_{t\rightarrow t_{i+1}^-}\mbox{${\bf r}$}'(t)\end{aligned}\end{align} \]

eru bæði til.

Líka sagt að stikaferillinn $\mbox{${\bf r}$}$ sé samfellt diffranlegur á köflum.

5.5. Heildi vigursviðs eftir ferli¶

5.5.1. Skilgreining¶

Látum $\mbox{${\bf F}$}(x,y)$ vera vigursvið og $\mbox{${\bf r}$}:[a,b]\rightarrow {\mathbb R}^2$ stikun á ferli $\cal C$ og gerum ráð fyrir að stikaferillinn $\mbox{${\bf r}$}$ sé samfellt diffranlegur á köflum. Heildi vigursviðsins $\mbox{${\bf F}$}(x,y)$ eftir ferlinum $\cal C$ er skilgreint sem

\[ \begin{align}\begin{aligned}\displaystyle\\\int_{\cal C} \mbox{${\bf F}$}\cdot d\mbox{${\bf r}$}= \int_{\cal C} \mbox{${\bf F}$}\cdot \mbox{${\bf T}$}\,ds =\int_a^b \mbox{${\bf F}$}(\mbox{${\bf r}$}(t))\cdot \mbox{${\bf r}$}'(t)\,dt.\end{aligned}\end{align} \]

5.5.2. Skilgreining¶

Ritum $\mbox{${\bf F}$}(x,y)=F_1(x,y)\,\mbox{${\bf i}$}+F_2(x,y)\,\mbox{${\bf j}$}$. Ritum líka $\mbox{${\bf r}$}(t)=x(t)\,\mbox{${\bf i}$}+y(t)\,\mbox{${\bf j}$}$. Þá má rita $dx=x'(t)\,dt,\, dy=y'(t)\,dt$. Með því að nota þennan rithátt fæst að

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} \int_{\cal C}\mbox{${\bf F}$}\cdot d\mbox{${\bf r}$}&=\int_a^b (F_1(x,y)\,\mbox{${\bf i}$}+F_2(x(t),y(t))\,\mbox{${\bf j}$})\cdot(x'(t)\,\mbox{${\bf i}$}+y'(t)\,\mbox{${\bf j}$})\,dt\\ &=\int_a^b F_1(x(t),y(t))x'(t)\,dt+F_2(x(t),y(t))y'(t)\,dt\\ &=\int_{\cal C} F_1(x,y)\,dx+F_2(x,y)\,dy.\end{aligned}\end{split}\end{aligned}\end{align} \]

Athugasemd

Látum $\cal C$ vera feril í ${\mathbb R}^2$. Gerum ráð fyrir að $\mbox{${\bf r}$}_1:[a,b]\rightarrow {\mathbb R}^2$ og $\mbox{${\bf r}$}_2:[a',b']\rightarrow {\mathbb R}^2$ séu tveir samfellt diffranlegir á köflum stikaferlar sem stika $\cal C$. Gerum ennfremur ráð fyrir að $\mbox{${\bf r}$}_1(a)=\mbox{${\bf r}$}_2(b')$ og $\mbox{${\bf r}$}_1(b)=\mbox{${\bf r}$}_2(a')$ (þ.e.a.s. stikaferlarnir fara í sitthvora áttina eftir $\cal C$). Þá gildir ef $\mbox{${\bf F}$}(x,y)$ er vigursvið að

\[\displaystyle \int_{\cal C} \mbox{${\bf F}$}\cdot d\mbox{${\bf r}$}_1=-\int_{\cal C} \mbox{${\bf F}$}\cdot d\mbox{${\bf r}$}_2.\]

(Ef breytt er um stefnu á stikun á breytist formerki þegar vigursvið heildað eftir ferlinum.)

5.6. Ferilheildi og stigulsvið¶

5.6.1. Setning¶

Látum $\mbox{${\bf F}$}(x,y)$ vera samfellt stigulsvið skilgreint á svæði $D$ í ${\mathbb R}^2$ og látum $\varphi$ vera fall skilgreint á $D$ þannig að $\mbox{${\bf F}$}(x,y)=\nabla \varphi(x,y)$ fyrir alla punkta $(x,y)\in D$. Látum $\mbox{${\bf r}$}:[a,b]\rightarrow D$ vera stikaferill sem er samfellt diffranlegur á köflum og stikar feril $\cal C$ í $D$. Þá er

\[\displaystyle \int_{\cal C} \mbox{${\bf F}$}\cdot \,d\mbox{${\bf r}$}=\varphi(\mbox{${\bf r}$}(b))-\varphi(\mbox{${\bf r}$}(a)).\]

(Samsvarandi gildir fyrir vigursvið skilgreint á svæði $D\subseteq {\mathbb R}^3$.)

5.6.2. Fylgisetning¶

Látum $\mbox{${\bf F}$}$ vera samfellt stigulsvið skilgreint á mengi $D\subseteq {\mathbb R}^2$. Látum $\mbox{${\bf r}$}:[a,b]\rightarrow D$ vera stikaferil sem er samfellt diffranlegur á köflum og lokaður (þ.e.a.s. $\mbox{${\bf r}$}(a)=\mbox{${\bf r}$}(b)$) og stikar feril $\mathcal{C}$. Þá er

\[\displaystyle \oint_{\cal C} \mbox{${\bf F}$}\cdot \,d\mbox{${\bf r}$}=0.\]

(Ath. að rithátturinn

\[\displaystyle \oint_{\cal C}\]

er gjarnan notaður þegar heildað er yfir lokaðan feril $\cal C$.)

5.6.3. Fylgisetning¶

Látum $\mbox{${\bf F}$}$ vera samfellt stigulsvið skilgreint á mengi $D\subseteq {\mathbb R}^2$. Látum $\mbox{${\bf r}$}_1:[a_1,b_1]\rightarrow D$ og $\mbox{${\bf r}$}_2:[a_2,b_2]\rightarrow D$ vera stikaferla sem eru samfellt diffranlegir á köflum og stika ferlana $\mathcal{C}_1$ og $\mathcal{C}_2$. Gerum ráð fyrir að $\mbox{${\bf r}$}_1(a_1)=\mbox{${\bf r}$}_2(a_2)$ og $\mbox{${\bf r}$}_1(b_1)=\mbox{${\bf r}$}_2(b_2)$, þ.e.a.s. stikaferlarnir $\mbox{${\bf r}$}_1$ og $\mbox{${\bf r}$}_2$ hafa sameiginlega upphafs- og endapunkta. Þá er

\[\displaystyle \int_{{\cal C}_1} \mbox{${\bf F}$}\cdot\,d\mbox{${\bf r}$}_1=\int_{{\cal C}_2} \mbox{${\bf F}$}\cdot\,d\mbox{${\bf r}$}_2.\]

5.6.4. Skilgreining¶

Segjum að heildi vigursviðs $\mbox{${\bf F}$}$ sé óháð stikaferli ef fyrir sérhverja tvo samfellt diffranlega á köflum stikaferla $\mbox{${\bf r}$}_1$ og $\mbox{${\bf r}$}_2$ með sameiginlega upphafs- og endapunkta sem stika ferlana $\mathcal{C}_1$ og $\mathcal{C}_2$ gildir að

\[ \begin{align}\begin{aligned}\displaystyle\\\int_{{\cal C}_1} \mbox{${\bf F}$}\cdot\,d\mbox{${\bf r}$}_1= \int_{{\cal C}_2} \mbox{${\bf F}$}\cdot\,d\mbox{${\bf r}$}_2.\end{aligned}\end{align} \]

5.6.5. Setning¶

Ferilheildi samfellds vigursviðs $\mbox{${\bf F}$}$ er óháð stikaferli ef og aðeins ef $\oint_{\cal C} \mbox{${\bf F}$}\cdot\,d\mbox{${\bf r}$}=0$ fyrir alla lokaða ferla $\cal C$ sem eru samfellt diffranlegir á köflum.

5.6.6. Upprifjun¶

Segjum að mengi $D\subseteq {\mathbb R}^2$ sé ferilsamanhangandi (e. connected, path-connected) ef fyrir sérhverja tvo punkta $P, Q\in D$ gildir að til er stikaferill $\mbox{${\bf r}$}:[0,1]\rightarrow D$ þannig að $\mbox{${\bf r}$}(0)=P$ og $\mbox{${\bf r}$}(1)=Q$.

5.6.7. Setning¶

Látum $D$ vera opið mengien: open set.
Smelltu fyrir ítarlegri þýðingu. í ${\mathbb R}^2$ sem er ferilsamanhangandi. Ef $\mbox{${\bf F}$}$ er samfellt vigursvið skilgreint á $D$ og ferilheildi $\mbox{${\bf F}$}$ eru óháð vegi þá er $\mbox{${\bf F}$}$ stigulsvið.

5.6.8. Setning¶

Fyrir samfellt vigursvið $\mbox{${\bf F}$}$ skilgreint á opnu ferilsamanhangandi mengi $D\subseteq {\mathbb R}^2$ er eftirfarandi jafngilt:

$\mbox{${\bf F}$}$ er stigulsvið,
$\oint_{\cal C} \mbox{${\bf F}$}\cdot\,d\mbox{${\bf r}$}=0$ fyrir alla samfellt diffranlega á köflum lokaða stikaferla $\mbox{${\bf r}$}$ í $D$,
Ferilheildi $\mbox{${\bf F}$}$ er óháð vegi.

Sýna sönnun

5.7. Fletir¶

5.7.1. Óformleg skilgreining¶

Flöturen: face.
Smelltu fyrir ítarlegri þýðingu. $\cal S$ í ${\mathbb R}^3$ er ,,tvívítt“ hlutmengi í ${\mathbb R}^3$.

5.7.2. Lýsing¶

Flötum er aðallega lýst með formúlum á þrjá vegu:

Gefið er fall $f(x,y,z)$. Fletinum $\cal S$ er lýst með jöfnu $f(x,y,z)=C$ (þ.e.a.s. $\cal S$ er jafnhæðarflöturen: contour surface.
Smelltu fyrir ítarlegri þýðingu. fallsins $f$). Þá er

\[\displaystyle {\cal S}=\{(x,y,z)\mid f(x,y,z)=C\}.\]
Gefið er fall skilgreint á ferilsamanhangandi svæði $D$ í ${\mathbb R}^2$. Fletinum $\cal S$ er lýst sem grafi fallsins $f$. Þá er

\[\displaystyle {\cal S}=\{(x,y,z)\mid (x,y)\in D\mbox{ og } z=f(x,y)\}.\]
Með stikafleti (sjá næstu grein).

5.8. Stikafletir¶

5.8.1. Skilgreining¶

Látum $D$ vera ferilsamanhangandi hlutmengi í ${\mathbb R}^2$. Samfelld vörpun $\mbox{${\bf r}$}:D\rightarrow {\mathbb R}^3; \mbox{${\bf r}$}(u,v)=\big(x(u,v), y(u,v), z(u,v)\big)$ þannig að

\[\displaystyle {\cal S}=\{\mbox{${\bf r}$}(u,v)\mid (u,v)\in D\}\]

er flötur kallast stikaflötur. Segjum að $\mbox{${\bf r}$}$ sé stikun á fletinum $\cal S$. Viljum að $\mbox{${\bf r}$}$ sé eintæk vörpun, nema hugsanlega á jaðri $D$. Ritum einnig

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial \mbox{${\bf r}$}}{\partial u}= \bigg(\frac{\partial x}{\partial u}, \frac{\partial y}{\partial u}, \frac{\partial z}{\partial u}\bigg)\quad\mbox{ og }\quad \frac{\partial \mbox{${\bf r}$}}{\partial v}= \bigg(\frac{\partial x}{\partial v}, \frac{\partial y}{\partial v}, \frac{\partial z}{\partial v}\bigg).\end{aligned}\end{align} \]

5.9. Snertiplön¶

5.9.1. Setning¶

Látum $\cal S$ vera flöt sem er gefinn sem jafnhæðarflöturen: contour surface.
Smelltu fyrir ítarlegri þýðingu. $f(x,y,z)=C$. Ef $(a, b, c)$ er punktur á fletinum og fallið $f$ er diffranlegt í punktinum $(a, b,c)$ þá er vigurinn $\mbox{${\bf n}$}=\nabla f(a, b, c)$ hornréttur á flötinn í punktinum $(a,b, c)$ og ef $\nabla f(a, b, c)\neq \mbox{${\bf 0}$}$ þá hefur flöturinn snertiplanen: tangent plane.
Smelltu fyrir ítarlegri þýðingu. í punktinum. Jafna snertiplansins er

\[\displaystyle f_1(a, b, c)x+f_2(a, b, c)y+f_3(a, b, c)z=D\]

þar sem

\[ \begin{align}\begin{aligned}\displaystyle\\D= f_1(a, b, c)a+f_2(a, b, c)b +f_3(a, b, c)c.\end{aligned}\end{align} \]
Látum $\cal S$ vera flöt sem er gefinn sem graf falls $z=f(x,y)$. Ef $(a, b, f(a,b))$ er punktur á fletinum og fallið $f$ er diffranlegt í punktinum $(a, b)$ þá er vigurinn

\[\displaystyle \mbox{${\bf n}$}=\big(0 ,1 ,f_2(a, b)\big)\times\big(1 ,0 ,f_1(a, b)\big)=\big(f_1(a, b), f_2(a, b), -1\big)\]

hornréttur á flötinn í punktinum $(a,b, f(a,b))$ og flöturinn hefur snertiplan í punktinum. Jafna snertiplansins er

\[\displaystyle z=f(a, b)+f_1(a, b)(x-a)+f_2(a, b)(y-b).\]

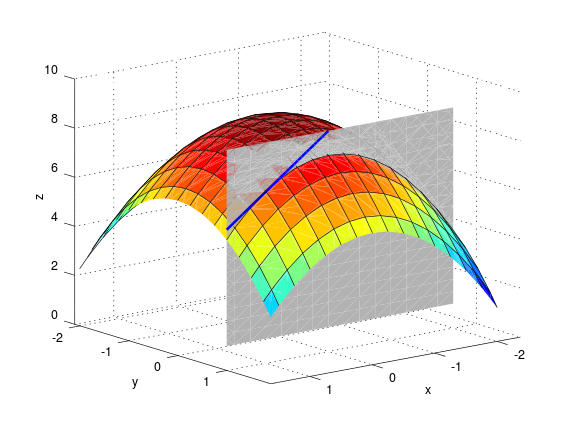
Snertivigur við skurðferil sléttunnar $y=b$ og yfirborðsins $z = f(x,y)$ í punktinum $(a,b,f(a,b))$ er $\mathbf{T}_1 = (1,0,f_1(a,b))$.

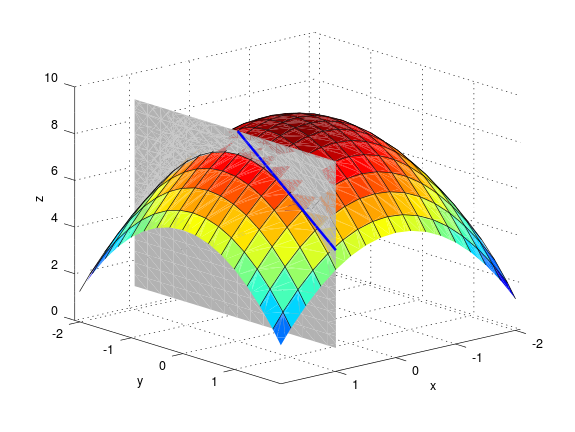
Snertivigur við skurðferil sléttunnar $x=a$ og yfirborðsins $z = f(x,y)$ í punktinum $(a,b,f(a,b))$ er $\mathbf{T}_2 = (0,1,f_2(a,b))$.

Látum $\mbox{${\bf r}$}: D\subseteq {\mathbb R}^2\rightarrow {\mathbb R}^3$ vera stikaflöt. Ef $(x_0, y_0, z_0)=\mbox{${\bf r}$}(u_0, v_0)$ er punktur á fletinum sem $\mbox{${\bf r}$}(u,v)=\big(x(u,v), y(u,v), z(u,v)\big)$ stikar og föllin $x(u,v), y(u,v), z(u,v)$ eru diffranleg í punktinum $(x_0, y_0)$ þá er vigurinn

\[ \begin{align}\begin{aligned}\displaystyle\\\mbox{${\bf n}$}=\frac{\partial \mbox{${\bf r}$}}{\partial u}\times \frac{\partial \mbox{${\bf r}$}}{\partial v}\end{aligned}\end{align} \]

reiknaður með $u=u_0$ og $v=v_0$ þvervigur á flötinn í punktinum $(x_0, y_0, z_0)$.

5.9.2. Skilgreining¶

Ef vigrarnir $\frac{\partial \mbox{${\bf r}$}}{\partial u}(u,v)$ og $\frac{\partial \mbox{${\bf r}$}}{\partial v}(u,v)$ eru óháðir fyrir alla punkta $(u,v)\in D$ þá er sagt að stikunin sé regluleg.

Athugasemd

Ef vigrarnir $\frac{\partial \mbox{${\bf r}$}}{\partial u}(u_0,v_0)$ og $\frac{\partial\mbox{${\bf r}$}}{\partial v}(u_0,v_0)$ eru óháðir þá spanna þeir snertiplan við flötinn í punktinum $\mbox{${\bf r}$}(u_0,v_0)$. Snertiplanið hefur stikun

\[\displaystyle \Pi(u,v) = \mbox{${\bf r}$}(u_0,v_0)+u\frac{\partial \mbox{${\bf r}$}}{\partial u}(u_0,v_0)+v\frac{\partial \mbox{${\bf r}$}}{\partial v}(u_0,v_0).\]

5.10. Flatarheildi¶

5.10.1. Verkefni¶

Flatarmál flata – sambærilegt við bogalengd ferla.
Heildi falls yfir flöt með tilliti til flatarmáls – sambærilegt við heildi falls eftir ferli með tilliti til bogalengdar.
Heildi vigursviðs yfir flöt – svipar til heildis vigursviðs eftir ferli.

5.11. Flatarmál flata¶

5.11.1. Skilgreining¶

Látum $\mbox{${\bf r}$}:D\rightarrow {\mathbb R}^2$ vera reglulegan stikaflöt sem stikar flöt $\cal S$. Flatarmál $\cal S$ er

\[ \begin{align}\begin{aligned}\displaystyle\\A=\int\!\!\!\int_D\,dS=\int\!\!\!\int_D \big|{\textstyle\frac{\partial \mbox{${\bf r}$}}{\partial u} \times\frac{\partial \mbox{${\bf r}$}}{\partial v}}\big|\,dudv.\end{aligned}\end{align} \]

5.11.2. Formúla¶

Látum $f(x,y)$ vera diffranlegt fall skilgreint á mengi $D$ í ${\mathbb R}^2$. Flatarmál grafsins $z=f(x,y)$ er gefið með formúlunni

\[ \begin{align}\begin{aligned}\displaystyle\\A=\int\!\!\!\int_D dS=\int\!\!\!\int_D {\textstyle\sqrt{1+ \big(\frac{\partial f}{\partial x}\big)^2+ \big(\frac{\partial f}{\partial y}\big)^2}}\,\,dx\,dy.\end{aligned}\end{align} \]

5.11.3. Skilgreining¶

Látum $\mbox{${\bf r}$}:D\rightarrow {\mathbb R}^3$ vera reglulegan stikaflöt sem stikar flöt $\cal S$. Flatarmál $\cal S$ er

\[ \begin{align}\begin{aligned}\displaystyle\\A=\int\!\!\!\int_D\,dS=\int\!\!\!\int_D \big|{\textstyle\frac{\partial \mbox{${\bf r}$}}{\partial u} \times\frac{\partial \mbox{${\bf r}$}}{\partial v}}\big|\,dudv.\end{aligned}\end{align} \]

5.11.4. Formúla¶

Látum $f(x,y)$ vera diffranlegt fall skilgreint á mengi $D$ í ${\mathbb R}^2$. Flatarmál grafsins $z=f(x,y)$ er gefið með formúlunni

\[ \begin{align}\begin{aligned}\displaystyle\\A=\int\!\!\!\int_D dS=\int\!\!\!\int_D {\textstyle\sqrt{1+ \big(\frac{\partial f}{\partial x}\big)^2+ \big(\frac{\partial f}{\partial y}\big)^2}}\,\,dx\,dy.\end{aligned}\end{align} \]

5.11.5. Formúlur¶

Ritum $dS$ fyrir flatarmálselement á fleti $\cal S$.

Ef $\mbox{${\bf r}$}:D\subseteq{\mathbb R}^2\rightarrow {\mathbb R}^3$ er stikun á $\cal S$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\dS=\bigg|\frac{\partial \mbox{${\bf r}$}}{\partial u}\times\frac{\partial \mbox{${\bf r}$}}{\partial v}\bigg|\,du\,dv.\end{aligned}\end{align} \]
Ef $\cal S$ er graf $z=g(x,y)$ þá er

\[\displaystyle dS=\sqrt{1+g_1(x,y)^2+g_2(x,y)^2}\,dx\,dy.\]
Gerum ráð fyrir að flöturinn $\cal S$ í ${\mathbb R}^3$ hafi þann eiginleika að ofanvarp hans á $xy$-planið sé eintækt eða með öðrum orðum hægt er að lýsa fletinum sem grafi $z=f(x,y)$. Ef $\mbox{${\bf n}$}$ er þvervigur á flötinn og $\gamma$ er hornið sem þvervigurinnen: normal vector.
Smelltu fyrir ítarlegri þýðingu. $\mbox{${\bf n}$}$ myndar við jákvæða hluta $z$-ássins þá er

\[ \begin{align}\begin{aligned}\displaystyle\\dS=\bigg|\frac{1}{\cos\gamma}\bigg|\,dx\,dy =\frac{|\mbox{${\bf n}$}|}{|\mbox{${\bf n}$}\cdot\mbox{${\bf k}$}|}\,dx\,dy.\end{aligned}\end{align} \]

Í þessu tilviki gildir einnig að ef $\cal S$ er lýst sem hæðarfleti $G(x,y,z)=C$ þá er

\[\displaystyle dS=\bigg|\frac{\nabla G(x,y,z)}{G_3(x,y,z)}\bigg|\,dx\,dy.\]

5.11.6. Skilgreining¶

Látum $\mbox{${\bf r}$}: D\rightarrow {\mathbb R}^3$ vera reglulega stikun á fleti $\cal S$. Heildi falls $f(x,y,z)$ yfir flötinn $\cal S$ með tilliti til flatarmáls er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_{\cal S} f\,dS=\int\!\!\!\int_D f(\mbox{${\bf r}$}(u,v)) \big|{\textstyle\frac{\partial \mbox{${\bf r}$}}{\partial u} \times\frac{\partial \mbox{${\bf r}$}}{\partial v}}\big|\,dudv.\end{aligned}\end{align} \]

5.12. Einingarþvervigrasvið¶

5.12.1. Skilgreining¶

Látum $\cal S$ vera flöt í ${\mathbb R}^3$ sem hefur snertiplanen: tangent plane.
Smelltu fyrir ítarlegri þýðingu. í punkti $P$. Einingarþvervigur $\mbox{${\bf n}$}$ á flötinn $\cal S$ í punktinum $P$ er einingarviguren: normalized vector.
Smelltu fyrir ítarlegri þýðingu. hornréttur á snertiplan við flötinn í punktinum $P$.

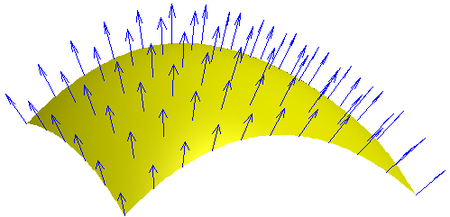
Einingarþvervigrasvið á $\cal S$ er samfellt vigursviðen: vector field.
Smelltu fyrir ítarlegri þýðingu. $\mbox{${\bf N}$}$ sem er skilgreint í öllum punktum $\cal S$ þannig að fyrir $(x,y,z)\in{\cal S}$ er vigurinn $\mbox{${\bf n}$}(x,y,z)$ einingarvigur sem er hornréttur á snertiplan við flötinn í punktinum $(x,y,z)$.

5.13. Áttanlegir fletir¶

5.13.1. Skilgreining¶

Flöturinn $\cal S$ er sagður áttanleguren: orientable.
Smelltu fyrir ítarlegri þýðingu. ef til er einingarþvervigrasvið $\mbox{${\bf N}$}$ á $\cal S$.

Áttunen: orientation.
Smelltu fyrir ítarlegri þýðingu. á áttanlegum fleti felst í því að velja annað af tveimur mögulegum einingaþvervigrasviðum.

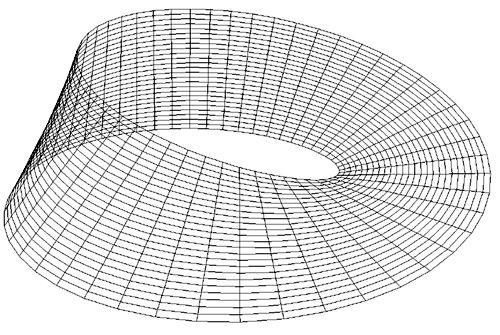
Möbiusarborði er ekki áttanlegur.

5.13.2. Umræða¶

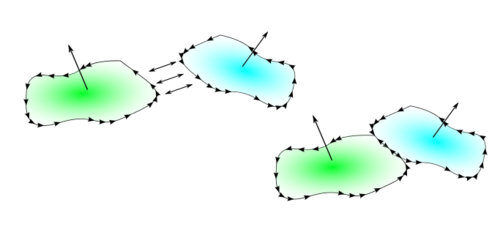
Ef áttanlegur flötur $\cal S$ hefur jaðar þá skilgreinir áttunin stefnu á jaðri $\cal S$. Venjan er að velja stefnu jaðarsins þannig að þegar gengið er eftir honum sé einingarþvervigrasviðið á vinstri hönd (hægri handar regla).

Ef tveir áttanlegir fletir hafa jaðar má splæsa þeim saman í áttanlegan flöt með því að líma þá saman á (hluta af) jöðrunum og gæta þess að jaðrarnir hafi andstæða stefnu á samskeytunum.

5.13.3. Setning¶

Gerum ráð fyrir að $\cal S$ sé áttanleguren: orientable.
Smelltu fyrir ítarlegri þýðingu. flötur og $\mbox{${\bf r}$}:D\subseteq{\mathbb R}^2\rightarrow {\mathbb R}^3$ sé regluleg stikun á $\cal S$ (það er, $\frac{\partial \mbox{${\bf r}$}}{\partial u}$ og $\frac{\partial \mbox{${\bf r}$}}{\partial v}$ eru samfelld föll af $u$ og $v$ og vigrarnir $\frac{\partial \mbox{${\bf r}$}}{\partial u}$ og $\frac{\partial \mbox{${\bf r}$}}{\partial v}$ eru línulega óháðir). Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\mbox{${\bf N}$}= \frac{\frac{\partial \mbox{${\bf r}$}}{\partial u}\times\frac{\partial \mbox{${\bf r}$}}{\partial v}} {|\frac{\partial \mbox{${\bf r}$}}{\partial u}\times\frac{\partial \mbox{${\bf r}$}}{\partial v}|}\end{aligned}\end{align} \]

einingarþvervigrasvið á $\cal S$.

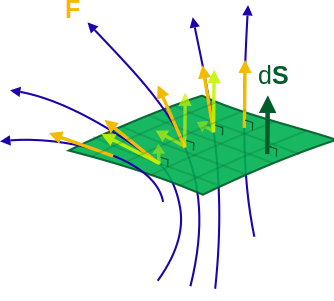
5.14. Heildi vigursviðs yfir flöt - Flæði¶

5.14.1. Skilgreining og ritháttur¶

Látum $\cal S$ vera áttanleganen: orientable.
Smelltu fyrir ítarlegri þýðingu. flöt stikaðan af reglulegum stikaferli $\mbox{${\bf r}$}:D\subseteq{\mathbb R}^2\rightarrow {\mathbb R}^3$ með samfelldar hlutafleiður. Látum $\mbox{${\bf N}$}$ tákna einingarþvervigrasviðið sem gefið er í Setningu 5.13.3. Heildi vigursviðs $\mbox{${\bf F}$}$ yfir flötinn $\cal S$ er skilgreint sem

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_{\cal S} \mbox{${\bf F}$}\cdot\mbox{${\bf N}$}\,dS =\int\!\!\!\int_D \mbox{${\bf F}$}(\mbox{${\bf r}$}(u,v))\cdot \bigg( \frac{\partial \mbox{${\bf r}$}}{\partial u}\times\frac{\partial \mbox{${\bf r}$}}{\partial v}\bigg)\, du\,dv.\end{aligned}\end{align} \]

Slík heildi eru oft nefnd flæðien: flux.
Smelltu fyrir ítarlegri þýðingu. vigursviðsins $\mbox{${\bf F}$}$ gegnum flötinn $\cal S$.

Ritum $d\mbox{${\bf S}$}=\mbox{${\bf N}$}\,dS$. Þá er

\[\displaystyle \int\!\!\!\int_{\cal S} \mbox{${\bf F}$}\cdot\mbox{${\bf N}$}\,dS=\int\!\!\!\int_{\cal S} \mbox{${\bf F}$}\cdot\,d\mbox{${\bf S}$}.\]

5.14.2. Samantekt¶

Ef $\mbox{${\bf r}$}:D\subseteq{\mathbb R}^2\rightarrow {\mathbb R}^3$ er stikun á $\cal S$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\d\mbox{${\bf S}$}=\pm \bigg(\frac{\partial \mbox{${\bf r}$}}{\partial u}\times\frac{\partial \mbox{${\bf r}$}}{\partial v}\bigg)\,du\,dv.\end{aligned}\end{align} \]
Ef $\cal S$ er graf $z=f(x,y)$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\d\mbox{${\bf S}$}=\pm\bigg(-\frac{\partial f}{\partial x},-\frac{\partial f}{\partial y},1\bigg)\,dx\,dy.\end{aligned}\end{align} \]
Gerum ráð fyrir að flöturinn $\cal S$ í ${\mathbb R}^3$ hafi þann eiginleika að ofanvarp hans á $xy$-planið sé eintækt eða með öðrum orðum hægt er að lýsa fletinum sem grafi $z=f(x,y)$. Ef fletinum $\cal S$ er lýst sem hæðarfleti $G(x,y,z)=C$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\d\mbox{${\bf S}$}=\pm\frac{\nabla G(x,y,z)}{|\nabla G(x,y,z)|}\,dS= \pm\frac{\nabla G(x,y,z)}{G_3(x,y,z)}\,dx\,dy.\end{aligned}\end{align} \]

Val á áttunen: orientation.
Smelltu fyrir ítarlegri þýðingu. felst í því að velja $+$ eða $-$ í formúlunum hér að ofan.

5.14.3. Túlkun¶

Hugsum okkur að vigursviðið $\mbox{${\bf F}$}$ lýsi streymi vökva. Hugsum svo flötinn $\cal S$ sem himnu sem vökvinn getur streymt í gegnum. Áttun á $\cal S$ gefur okkur leið til að tala um hliðar flatarins og að vökvinn streymi í gegnum flötinn frá einni hlið til annarrar. Streymi vökvans gegnum flötinn (rúmmál per tímaeiningu) er gefið með heildinu $\int\!\!\!\int_{\cal S} \mbox{${\bf F}$}\cdot\mbox{${\bf N}$}\,dS$ þar sem streymi í stefnu $\mbox{${\bf N}$}$ reiknast jákvætt.