4. Margföld heildi¶

A bruise is a lesson… and each lesson makes us better.

- George R.R. Martin, A Game of Thrones

4.1. Skiptingar¶

4.1.1. Skilgreining¶

Látum $R=[a,b]\times[c,d]$ vera rétthyrning í planinu. Skipting $P$ á rétthyrningnum $R$ felst í því að taka skiptingar

\[ \begin{align}\begin{aligned}\displaystyle\\a=x_0<x_1<\cdots<x_m=b\qquad\mbox{og}\qquad c=y_0<y_1<\cdots<y_n=d\end{aligned}\end{align} \]

á bilunum $[a,b]$ og $[c,d]$ og nota þær skiptingar til að skipta $R$ upp í rétthyrninga $[x_i,x_{i+1}]\times [y_j,y_{j+1}]$. Ritum $\Delta x_i=x_{i+1}-x_i$ og $\Delta y_j=y_{j+1}-y_j$. Norm skiptingarinnar $P$, táknað með $\|P\|$, er skilgreint sem lengd lengstu hornalínu í rétthyrningunum $[x_i,x_{i+1}]\times [y_j,y_{j+1}]$.

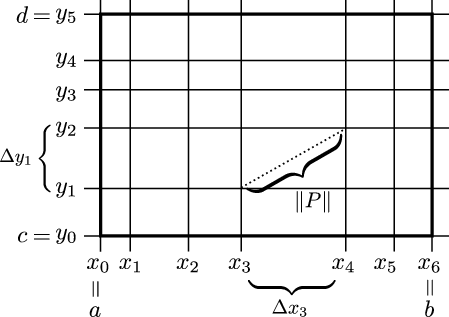
Skipting $P$ á rétthyrningi $R= [a,b]\times [c,d]$.

4.2. Riemann-summa¶

4.2.1. Skilgreining¶

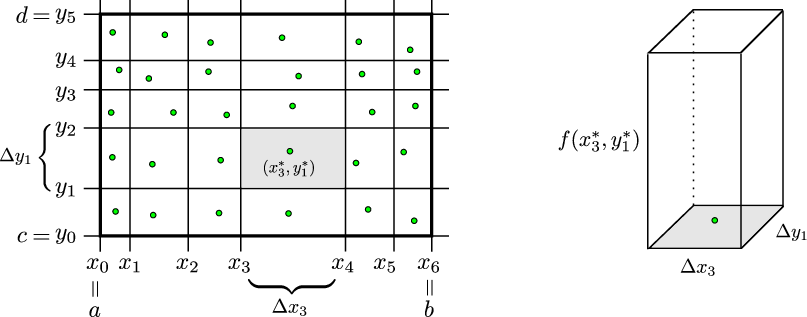
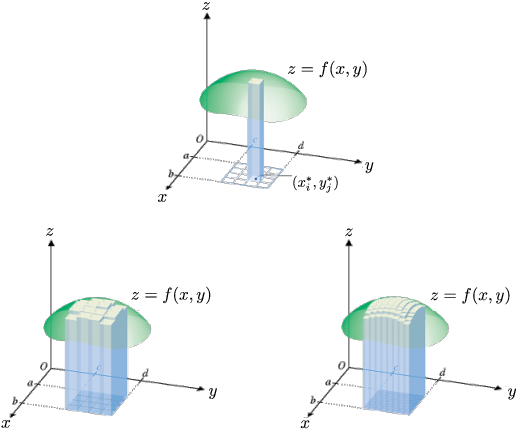
Látum $f$ vera fall skilgreint á rétthyrningi $R=[a,b]\times[c,d]$ og látum $P$ vera skiptingu á $R$. Veljum úr hverjum rétthyrningi $[x_i,x_{i+1}]\times [y_j,y_{j+1}]$ punkt $(x_i^*, y_j^*)$. Skilgreinum Riemann-summuna

\[ \begin{align}\begin{aligned}\displaystyle\\\mathcal{R}(f,P)=\sum_{i=1}^m\sum_{j=1}^n f(x_i^*, y_j^*)\Delta x_i\Delta y_j.\end{aligned}\end{align} \]

4.3. Tvöfalt heildi yfir rétthyrning¶

4.3.1. Skilgreining¶

Sagt er að fall $f$ skilgreint á rétthyrningi $R=[a,b]\times [c,d]$ sé heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. yfir $R$ með heildien: integral.
Smelltu fyrir ítarlegri þýðingu. $I$ (hér stendur $I$ fyrir tölu) ef fyrir sérhvert $\varepsilon>0$ er til tala $\delta>0$ þannig að $|\mathcal{R}(f,P)-I|<\varepsilon$ fyrir allar skiptingar $P$ með $\|P\|<\delta$ óháð vali á punktunum $(x_i^*, y_j^*)$.

Ritum þá

\[\displaystyle \int\!\!\!\int_R f(x,y)dA=I.\]

4.4. Tvöfalt heildi yfir takmarkað svæði¶

4.4.1. Skilgreining¶

Látum $D$ vera takmarkað svæði í planinu. Fall $f$ er sagt heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. yfir $D$ ef til er rétthyrningur $R$ sem inniheldur $D$ og fallið

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\hat{f}(x,y)=\left\{\begin{array}{rcl} f(x,y)& & \mbox{ef }(x,y)\in D,\\ 0& & \mbox{ef }(x,y)\in R\setminus D \end{array}\right.\end{split}\end{aligned}\end{align} \]

er heildanlegt yfir $R$.

4.4.2. Setning¶

Látum $f$ vera samfellt fall skilgreint á lokuðu og takmörkuðu svæði $D$ í planinu ${\mathbb R}^2$. Gerum ráð fyrir að jaðar $D$ samanstandi af endanlega mörgum ferlum sem hafa endanlega lengd. Þá er fallið $f$ heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. yfir $D$.

4.4.3. Setning¶

Látum $D$ vera svæði í planinu og $f$ takmarkaðen: bounded.
Smelltu fyrir ítarlegri þýðingu. fall skilgreint á $D$ og heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. yfir $D$. Þá gildir:

$\int\!\!\!\int_D f(x,y)\,dA=0$ ef flatarmál $D$ er 0.
$\int\!\!\!\int_D 1\,dA=$ flatarmál $D$.
Ef $f(x,y)\geq 0$ fyrir alla punkta $(x,y)$ í $D$ þá er $\int\!\!\!\int_D f(x,y)\,dA$ jafnt rúmmáli rúmskikans sem liggur milli $D$ og grafsins $z=f(x,y)$.
Ef $f(x,y)\leq 0$ fyrir alla punkta $(x,y)$ í $D$ þá er $\int\!\!\!\int_D f(x,y)\,dA$ jafnt mínus rúmmáli rúmskikans sem liggur milli $D$ og grafsins $z=f(x,y)$.

4.4.4. Setning¶

Ef $D$ er svæði í planinu og $f$ og $g$ heildanleg föll yfir $D$ þá gildir:

Ef $L$ og $M$ eru fastar þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_D Lf(x,y)+Mg(x,y)\,dA=L\!\int\!\!\!\int_D f(x,y)\,dA+M\!\int\!\!\!\int_D g(x,y)\,dA.\end{aligned}\end{align} \]
Ef $f(x,y)\leq g(x,y)$ þá er

\[\displaystyle \int\!\!\!\int_D f(x,y)\,dA\leq \int\!\!\!\int_Dg(x,y)\,dA.\]
Þríhyrningsójafna:

\[\bigg|\int\!\!\!\int_D f(x,y)\,dA\bigg|\leq \int\!\!\!\int_D |f(x,y)|\,dA.\]

Ritum $D$ sem sammengi af svæðum $D_1,\ldots, D_k$ sem skarast ekki nema mögulega í jaðarpunktum þá er

\[\displaystyle \int\!\!\!\int_D f(x,y)\,dA=\sum_{i=1}^k\int\!\!\!\int_{D_i}f(x,y)\,dA.\]

4.4.5. Setning Fubinis¶

Látum $f$ vera jákvætt fall sem er heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. á rétthyrningi $R=[a,b]\times [c,d]$. Setjum

\[\displaystyle A(x)=\int_c^d f(x,y)\,dy\qquad\mbox{($x$ hugsað sem fasti þegar heildað)}.\]

Þá gildir að

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_R f(x,y)\,dA=\int_a^b A(x)\,dx=\int_a^b\!\!\int_c^d f(x,y)\,dy\,dx.\end{aligned}\end{align} \]

Sömuleiðis gildir þegar við setjum

\[\displaystyle A(y)=\int_a^b f(x,y)\,dx\qquad\mbox{($y$ hugsað sem fasti þegar heildað)} \qquad \text{að}\]

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_R f(x,y)\,dA=\int_c^d A(y)\,dy=\int_c^d\!\!\int_a^b f(x,y)\,dx\,dy.\end{aligned}\end{align} \]

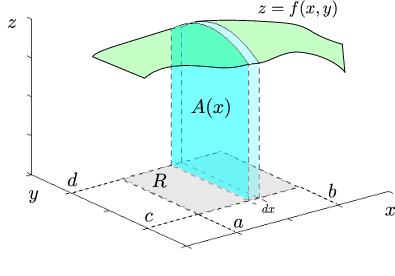
Athugasemd

Setning Fubinis er stundum kölluð brauðsneiðareglan. Ef við ímyndum okkur að rúmskikinn sem liggur milli graf jákvæðs falls og $xy$-sléttunnar sé brauðhleifur, þá má reikna rúmmál hans með því að skera hann í næfurþunnar brauðsneiðar sem liggja samsíða annað hvort $x$-ás eða $y$-ás, reikna svo rúmmál hverrar brauðsneiðar fyrir sig og leggja saman.

4.5. $x$-einföld og $y$-einföld svæði¶

4.5.1. Skilgreining¶

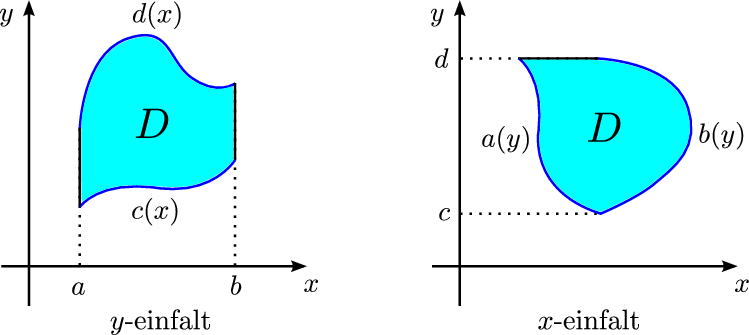
Svæði $D$ í planinu er sagt vera $y$-einfalt ef hægt er að finna tölur $a$ og $b$ og föll $c(x)$ og $d(x)$ þannig að

\[\displaystyle D=\{(x,y)\mid a\leq x\leq b, c(x)\leq y\leq d(x)\}.\]

Svæði $D$ í planinu er sagt vera $x$-einfalt ef hægt er að finna tölur $c$ og $d$ og föll $a(y)$ og $b(y)$ þannig að

\[\displaystyle D=\{(x,y)\mid c\leq y\leq d, a(y)\leq x\leq b(y)\}.\]

4.5.2. Regla¶

Lokað og takmarkað svæði $D$ í planinu er $y$-einfalt ef og aðeins ef sérhver lína af gerðinni $x=x_0$ sker $D$ í línustriki.

Lokað og takmarkað svæði $D$ er $x$-einfalt ef og aðeins ef sérhver lína af gerðinni $y=y_0$ sker svæðið í línustriki.

4.6. Heildi yfir $x$-einföld og $y$-einföld svæði¶

4.6.1. Setning¶

Látum $D=\{(x,y)\mid a\leq x\leq b, c(x)\leq y\leq d(x)\}$ vera $y$-einfalt svæði og $f(x,y)$ jákvætt fall sem er heildanlegt yfir $D$. Þá er

\[\displaystyle \int\!\!\!\int_D f(x,y)\,dA=\int_a^b\!\!\!\int_{c(x)}^{d(x)}f(x,y)\,dy\, dx.\]

Látum $D=\{(x,y)\mid c\leq y\leq d, a(y)\leq x\leq b(y)\}$ vera $x$-einfalt svæði og $f(x,y)$ jákvætt fall sem er heildanlegt yfir $D$. Þá er

\[\displaystyle \int\!\!\!\int_D f(x,y)\,dA=\int_c^d\!\!\!\int_{a(y)}^{b(y)}f(x,y)\,dx\, dy.\]

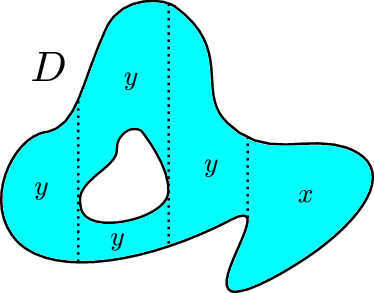
Hér er svæðinu $D$ skipt í endanlega mörg $x$-einföld og $y$-einföld svæði sem skarast eingöngu í punktum á jaðrinum.

4.7. Óeiginleg heildi¶

4.7.1. Umræða¶

Látum $f(x,y)\geq 0$ vera jákvætt fall sem er skilgreint á svæði $D$ í sléttunni. Ef

$D$ er ótakmarkað svæði eða
$f(x,y)$ er ótakmarkað á $D$

má í sumum tilfellum skilgreina tvöfalda heildið af $f$ yfir $D$.

Það er gert með því að finna fyrst runu af stækkandi lokuðum og takmörkuðum mengjum $D_1 \subseteq D_2 \subseteq \cdots \subseteq D$ sem ’stefnir á’ $D$. Ef

\[\displaystyle \int\!\!\!\int_{D_n} f(x,y)\,dA\]

er vel skilgreint fyrir öll $n$ og hefur markgildi þegar $n\to \infty$ (fyrir allar ólíkar runur $(D_n)_{n\geq 1}$) þá skilgreinum við óeiginlega heildiðen: improper integral.
Smelltu fyrir ítarlegri þýðingu.

\[\displaystyle \int\!\!\!\int_{D} f(x,y)\,dA := \lim_{n\to \infty} \int\!\!\!\int_{D_n} f(x,y)\,dA .\]

4.7.2. Skilgreining¶

Látum $f$ vera fall sem er heildanlegt yfir svæði $D$ í ${\mathbb R}^2$. Meðalgildi fallsins $f$ á $D$ er skilgreint sem talan

\[\displaystyle \bar{f}=\frac{1}{\mbox{flatarmál }D}\int\!\!\!\int_D f(x,y)\,dA.\]

4.7.3. Skilgreining¶

Segjum að mengi $D\subseteq {\mathbb R}^2$ sé ferilsamanhangandi (e. path-connected) ef fyrir sérhverja tvo punkta $P, Q\in D$ gildir að til er stikaferill $\mbox{${\bf r}$}:[0,1]\rightarrow D$ þannig að $\mbox{${\bf r}$}(0)=P$ og $\mbox{${\bf r}$}(1)=Q$.

Aðvörun

Í bók er orðið connected notað fyrir hugtakið ferilsamanhangandi. Venjulega er orðið connected notað yfir annað hugtak, skylt en samt ólíkt.

4.7.4. Setning (Meðalgildissetningen: mean value theorem.
Smelltu fyrir ítarlegri þýðingu. fyrir tvöföld heildi)¶

Gerum ráð fyrir að $f$ sé samfellt fall sem er skilgreint á lokuðu, takmörkuðu og ferilsamanhangandi svæði $D$ í ${\mathbb R}^2$. Þá er til punktur $(x_0,y_0)$ í $D$ þannig að

\[\displaystyle \frac{1}{\mbox{flatarmál }D}\int\!\!\!\int_D f(x,y)\,dA=f(x_0,y_0).\]

4.8. Breytuskipti¶

4.8.1. Upprifjun¶

Látum $P=(x,y)\neq \mbox{${\bf 0}$}$ vera punkt í plani. Pólhniten: polar coordinates.
Smelltu fyrir ítarlegri þýðingu. $P$ er talnapar $[r,\theta]$ þannig að $r$ er fjarlægð $P$ frá $O=(0,0)$ og $\theta$ er hornið á milli striksins $\overline{OP}$ og $x$-ássins. (Hornið er mælt þannig að rangsælis stefna telst jákvæð, og leggja má við $\theta$ heil margfeldi af $2\pi$.)

4.8.2. Skilgreining¶

Pólhnitarétthyrningur í $xy$-planinu er svæði sem afmarkast af tveimur hringbogum $x^2+y^2=a^2$ og $x^2+y^2=b^2$ og tveimur hálflínum sem byrja í $(0,0)$ og mynda hornin $\alpha$ og $\beta$ við $x$-ásinn (Hornin eru mæld þannig að rangsælis stefna telst jákvæð.)

Gerum ráð fyrir að $0\leq a\leq b$ og að $0\leq\beta-\alpha\leq 2\pi$. Þá má lýsa pólhnitarétthyrningnum með því að nota pólhnit þannig að

\[\displaystyle D=\{[r,\theta]\mid 0\leq a\leq r\leq b, \alpha\leq \theta\leq\beta\}.\]

4.8.3. Setning¶

Ef $f$ er fall sem er heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. yfir pólhnitarétthyrning $D=\{[r,\theta]\mid 0\leq a\leq r\leq b, \alpha\leq \theta\leq\beta\}$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_D f(x,y)\,dA=\int_\alpha^\beta\!\!\!\int_{a}^{b} f(r\cos\theta,r\sin\theta)\,r\,dr\, d\theta.\end{aligned}\end{align} \]

4.8.4. Upprifjun¶

Látum $f$ vera fall skilgreint á bili $[\alpha,\beta]$. Jafnan $r=f(\theta)$ lýsir mengi allra punkta í planinu sem hafa pólhniten: polar coordinates.
Smelltu fyrir ítarlegri þýðingu. á forminu $[f(\theta),\theta]$ þar sem $\alpha\leq\theta\leq\beta$. Þetta mengi kallast pólhnitagraf fallsins $f$.

4.8.5. Setning¶

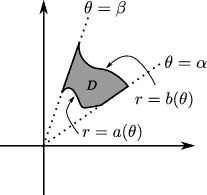
Látum $D$ vera svæði í $xy$-plani sem afmarkast af pólhnitalínum $\theta=\alpha$ og $\theta=\beta$ og tveimur pólhnitagröfum $r=a(\theta)$ og $r=b(\theta)$. Gerum ráð fyrir að $0\leq a(\theta)\leq r\leq b(\theta)$ og $0\leq \beta-\alpha\leq 2\pi$. Ef $f$ er heildanlegt fall yfir $D$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_D\,f(x,y)\,dA=\int_\alpha^\beta\!\!\!\int_{a(\theta)}^{b(\theta)} f(r\cos\theta,r\sin\theta)\,r\,dr\, d\theta.\end{aligned}\end{align} \]

4.8.6. Regla¶

Hugsum okkur að $f(x,y)$ sé fall og hægt sé að rita $f(x,y)=g(x)h(y)$. Látum $R=[a,b]\times [c,d]$. Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} \int\!\!\!\int_R f(x,y)\,dA&=\int_a^b\!\!\!\int_{c}^{d}g(x)h(y)\,dy\, dx\\ &=\bigg(\int_a^b g(x)\,dx\bigg)\bigg(\int_c^d h(y)\,dy\bigg).\end{aligned}\end{split}\end{aligned}\end{align} \]

4.8.7. Setning (Almenn breytuskiptaregla fyrir tvöföld heildi)¶

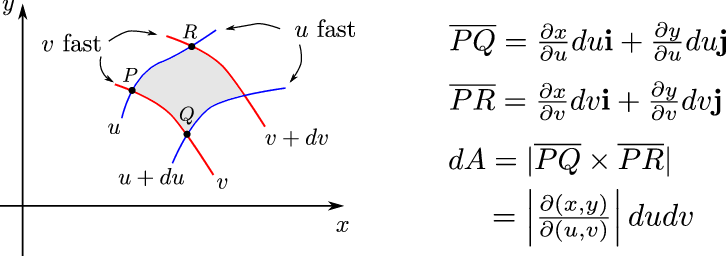
Látum $x=x(u,v)$, $y=y(u,v)$ vera gagntæka vörpun milli svæðis $S$ í $uv$-plani og svæðis $D$ í $xy$-plani. Gerum ráð fyrir að föllin $x(u,v)$, $y(u,v)$ hafi samfelldar fyrsta stigs hlutafleiður á $S$. Ef $f$ er heildanlegt fall yfir $D$, þá er fallið $g(u,v)=f(x(u,v), y(u,v))$ heildanlegt yfir $S$ og

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int_D f(x,y)\,dx\,dy=\int\!\!\!\int_S g(u,v) \bigg|\frac{\partial(x,y)}{\partial(u,v)}\bigg|\,du\,dv.\end{aligned}\end{align} \]

4.9. Þreföld heildi¶

4.9.1. Umræða¶

Heildien: integral.
Smelltu fyrir ítarlegri þýðingu. falls $f(x,y,z)$ yfir kassa $K=[a,b]\times[c,d]\times[u,v]$ í ${\mathbb R}^3$ er skilgreint á sambærilegan hátt og tvöfalt heildi er skilgreint.

Á sama hátt og fyrir tvöföld heildi má svo skilgreina heildi fyrir almennari rúmskikaEkki fannst þýðing á hugtakinu: rúmskiki~ í :math:`{mathbb R}^3.

Heildien: integral.
Smelltu fyrir ítarlegri þýðingu. falls $f(x,y,z)$ yfir rúmskikaEkki fannst þýðing á hugtakinu: rúmskika $R$ er táknað með

\[\displaystyle \int\!\!\!\int\!\!\!\int_R f(x,y,z)\,dV.\]

($dV$ stendur fyrir að heildað er með tilliti til rúmmáls.)

4.9.2. Setning¶

Látum $f(x,y,z)$ vera fall sem er heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. yfir kassa $K=[a,b]\times[c,d]\times[u,v]$ í ${\mathbb R}^3$. Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int\!\!\!\int_K f(x,y,z)\,dV= \int_a^b\!\int_c^d\!\int_u^v f(x,y,z)\,dz\,dy\,dx.\end{aligned}\end{align} \]

Breyta má röð heilda að vild, t.d. er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int\!\!\!\int_K f(x,y,z)\,dV= \int_u^v\!\int_c^d\!\int_a^b f(x,y,z)\,dx\,dy\,dz.\end{aligned}\end{align} \]

4.9.3. Setning¶

Látum $f(x,y,z)$ vera fall sem er heildanlegt yfir rúmskika $R$ og gerum ráð fyrir að $R$ hafi lýsingu á forminu

\[\displaystyle R=\{(x,y,z)\mid a\leq x\leq b,\ c(x)\leq y\leq d(x),\ u(x,y)\leq z\leq v(x,y)\}.\]

Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int\!\!\!\int_R f(x,y,z)\,dV= \int_a^b\!\int_{c(x)}^{d(x)}\!\int_{u(x,y)}^{v(x,y)} f(x,y,z)\,dz\,dy\,dx.\end{aligned}\end{align} \]

Breyturnar $x, y, z$ geta svo skipt um hlutverk.

4.9.4. Setning (Almenn breytuskiptaformúla fyrir þreföld heildi.)¶

Látum

\[\displaystyle (u,v,w)\mapsto (x(u,v,w), y(u,v,w), z(u,v,w))\]

vera gagntæka vörpun milli rúmskika $R$ í $xyz$-rúmi og rúmskika $S$ í $uvw$-rúmi. Gerum ráð fyrir að föllin $x(u,v,w), y(u,v,w), z(u,v,w)$ hafi öll samfelldar fyrsta stigs hlutafleiður. Ef $f(x,y,z)$ er fall sem er heildanlegt yfir $R$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} \int\!\!\!\int\!\!\!\int_R& f(x,y,z)\,dV \\&=\int\!\!\!\int\!\!\!\int_S f(x(u,v,w), y(u,v,w), z(u,v,w)) \bigg|\frac{\partial(x,y,z)}{\partial(u,v,w)}\bigg|\,du\,dv\,dw.\end{aligned}\end{split}\end{aligned}\end{align} \]

4.9.5. Skilgreining¶

Látum $(x,y,z)$ vera punkt í ${\mathbb R}^3$. Sívalningshniten: cylindrical coordinates.
Smelltu fyrir ítarlegri þýðingu. $(x,y,z)$ eru þrennd talna $r, \theta, z$ þannig að

\[\displaystyle x=r\cos\theta\qquad\qquad y=r\sin\theta\qquad\qquad z=z.\]

Athugasemd

Athugið að $[r,\theta]$ eru pólhnit punktsins $(x,y)$.

4.9.6. Setning (Breytuskipti yfir í sívalningshnit.)¶

Látum $R$ vera rúmskika í ${\mathbb R}^3$ og látum $f(x,y,z)$ vera heildanlegt fall yfir $R$. Gerum ráð fyrir að $R$ megi lýsa með eftirfarandi skorðum á sívalningshnit punktanna sem eru í $R$

\[\displaystyle \alpha\leq \theta\leq \beta,\ a(\theta)\leq r\leq b(\theta), u(r,\theta)\leq z\leq v(r,\theta),\]

þar sem $0\leq \beta-\alpha\leq 2\pi$. Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\int\!\!\!\int\!\!\!\int_R f(x,y,z)\,dV= \int_\alpha^\beta \!\int_{a(\theta)}^{b(\theta)}\int_{u(r,\theta)}^{v(r,\theta)} f(r\cos\theta,r\sin\theta,z)r\,dz\,dr\,d\theta.\end{aligned}\end{align} \]

4.10. Kúluhnit¶

4.10.1. Skilgreining¶

Látum $(x,y,z)$ vera punkt í ${\mathbb R}^3$. Kúluhniten: spherical coordinates.
Smelltu fyrir ítarlegri þýðingu. $(x,y,z)$ eru þrennd talna $\rho, \varphi, \theta$ þannig að

\[\displaystyle x=\rho\sin\varphi\cos\theta\qquad\qquad y=\rho\sin\varphi\sin\theta\qquad\qquad z=\rho\cos\varphi.\]

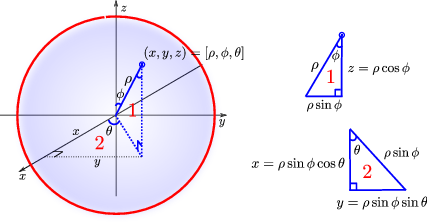
Punktur sem hefur kúluhnit $\rho, \varphi, \theta$ er táknaður með $[\rho, \varphi, \theta]$.

4.10.2. Umræða¶

Eftirfarandi jöfnur gefa aðferð til að finna kúluhniten: spherical coordinates.
Smelltu fyrir ítarlegri þýðingu.:

$\rho$ er fjarlægðin frá $(0,0,0)$ til $(x,y,z)$, það er að segja

\[\displaystyle \rho=\sqrt{x^2+y^2+z^2}.\]
$\varphi$ er hornið á milli jákvæða hluta $z$-ássins og línustriksins frá $(0,0,0)$ til $(x,y,z)$. Hornið $\varphi$ má ákvarða út frá jöfnunni

\[\displaystyle \tan\varphi=\frac{\sqrt{x^2+y^2}}{z}.\]
$\theta$ er hornið sem jákvæði hluti $x$-ásins myndar við línustrikið frá $(0,0,0)$ til $(x,y,0)$ (sama horn og notað í sívalningshnitum (og pólhnitum)). Hornið $\theta$ má finna út frá jöfnunni

\[\displaystyle \tan\theta=\frac{y}{x}.\]

Um kúluhnit $[\rho, \varphi, \theta]$ fyrir punkt $(x,y,z)$ gildir að velja má $\rho, \varphi, \theta$ þannig að $0\leq \rho$, $0\leq\varphi\leq \pi$ og $0\leq\theta\leq 2\pi$.

4.11. Breytuskipti í kúluhnit¶

4.11.1. Setning¶

Látum $R$ vera rúmskika þannig að þegar notuð eru kúluhniten: spherical coordinates.
Smelltu fyrir ítarlegri þýðingu. þá fæst eftirfarandi lýsing

\[ \begin{align}\begin{aligned}\displaystyle\\R=\{[\rho,\varphi,\theta]\mid \alpha\leq\theta\leq\beta, c\leq\varphi\leq d, a\leq \rho\leq b\}.\end{aligned}\end{align} \]

Ef $f$ er fall sem er heildanlegten: integrable.
Smelltu fyrir ítarlegri þýðingu. yfir $R$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} &\int\!\!\!\int\!\!\!\int_R f(x,y,z)\,dV=\\ &\int_\alpha^\beta\!\int_c^d\!\int_a^b f(\rho\sin\varphi\cos\theta, \rho\sin\varphi\sin\theta,\rho\cos\varphi) \,\rho^2\sin\varphi\,d\rho\,d\varphi\,d\theta.\end{aligned}\end{split}\end{aligned}\end{align} \]

4.12. Massamiðja¶

4.12.1. Regla¶

Látum $D$ tákna svæði í plani. Hugsum $D$ sem plötu þ.a. í punkti $(x,y)$ er efnisþéttleikinn gefinn með falli $\delta(x,y)$. Massi plötunnar er

\[\displaystyle m=\int\!\!\!\int_D \delta(x,y)\,dA.\]

Vægi plötunnar um línuna $x=0$ (þ.e. $y$-ás) og um línuna $y=0$ (þ.e. $x$-ás) eru gefin með

\[\displaystyle M_{x=0}=\int\!\!\!\int_D x\delta(x,y)\,dA \quad \text{og} \quad M_{y=0}=\int\!\!\!\int_D y\delta(x,y)\,dA.\]

Hnit massamiðju plötunnar eru $(\overline{x}, \overline{y})$ þar sem

\[\displaystyle \overline{x}=\frac{M_{x=0}}{m} \quad \text{og}\quad \overline{y}=\frac{M_{y=0}}{m}.\]

4.12.2. Regla¶

Látum $R$ tákna rúmskikaen: body.
Smelltu fyrir ítarlegri þýðingu.. Hugsum $R$ sem hlut þannig að í punkti $(x,y,z)$ er efnisþéttleikinn gefinn með falli $\delta(x,y,z)$. Massi hlutarins er

\[\displaystyle m=\int\!\!\!\int\!\!\!\int_R \delta(x,y,z)\,dV.\]

Vægi hlutarins um planið $x=0$ (þ.e. $yz$-planið) er

\[\displaystyle M_{x=0}=\int\!\!\!\int\!\!\!\int_R x\delta(x,y,z)\,dV.\]

Svipað skilgreinum við

\[\displaystyle M_{y=0}=\int\!\!\!\int\!\!\!\int_R y\delta(x,y,z)\,dV \quad \text{og}\quad M_{z=0}=\int\!\!\!\int\!\!\!\int_R z\delta(x,y,z)\,dV.\]

Hnit massamiðju hlutarins eru $(\overline{x}, \overline{y}, \overline{z})$ þar sem

\[ \begin{align}\begin{aligned}\displaystyle\\\overline{x}=\frac{M_{x=0}}{m} \qquad\mbox{og}\qquad \overline{y}=\frac{M_{y=0}}{m} \qquad\mbox{og}\qquad \overline{z}=\frac{M_{z=0}}{m}.\end{aligned}\end{align} \]

4.13. Hverfitregða¶

4.13.1. Regla¶

Látum $R$ tákna rúmskika. Hugsum $R$ sem hlut þannig að í punkti $(x,y,z)$ er efnisþéttleikinn gefinn með falli $\delta(x,y,z)$. Látum $L$ tákna línu (snúningsás) í rúminu. Hverfitregða hlutarins um $L$ er

\[\displaystyle I=\int\!\!\!\int\!\!\!\int_R D^2 \,\delta\,dV\]

þar sem $\delta=\delta(x,y,z)$ og $D=D(x,y,z)$ er fjarlægð punktsins $(x,y,z)$ frá $L$.

4.14. Yfirborðsflatarmál¶

4.14.1. Regla¶

Látum $D$ vera svæði í plani og $f(x,y)$ diffranlegt fall skilgreint á $D$. Flatarmál grafsins $z=f(x,y)$ þar sem $(x,y)\in D$ er gefið með formúlunni

\[\displaystyle S=\int\!\!\!\int_D \sqrt{1+f_1(x,y)^2+f_2(x,y)^2}\,dA.\]