1. Ferlar¶

1.2.1. Skilgreining¶

Vörpun \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}\) þannig að \(\mbox{${\bf r}$}(t)=(r_1(t),\ldots,r_n(t))\) kallast vigurgild vörpun. Slík vörpun er sögð samfelld ef föllin \(r_1, \ldots, r_n\) eru öll samfelld. Samfelld vörpun \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}\) er oft kölluð stikaferillen: parametric curve.
Smelltu fyrir ítarlegri þýðingu..

1.2.2. Ritháttur¶

Þegar fjallað er um stikaferil \(\mbox{${\bf r}$}: [a,b]\rightarrow {\mathbb R}^2\) þá er oft ritað

og þegar fjallað er um stikaferil \(\mbox{${\bf r}$}: [a,b]\rightarrow {\mathbb R}^3\) þá er oft ritað

1.3.1. Skilgreining¶

Ferill í planien: curve.
Smelltu fyrir ítarlegri þýðingu. er mengi punkta \((x,y)\) í planinu þannig að skrifa má \(x=f(t)\) og \(y=g(t)\) fyrir \(t\) á bili \(I\) þar sem \(f\) og \(g\) eru samfelld föll á \(I\). Auk þess liggur \((f(t),g(t))\) í punktamenginu fyrir öll \(t\in I\). Bilið \(I\) ásamt föllunum \((f,g)\) kallast stikun á ferlinum. Ferill í rúmi og stikunen: parametrization.
Smelltu fyrir ítarlegri þýðingu. á ferli í rúmi eru skilgreind á sambærilegan hátt.

1.3.2. Dæmi - Eðlisfræðileg túlkun¶

Líta má á veginn milli Reykjavíkur og Akureyrar sem feril.

Líta má á ferðalag eftir veginum frá Reykjavík til Akureyrar þar sem staðsetning er þekkt á hverjum tíma sem stikaferil þar sem tíminn er stikinn.

1.3.3. Dæmi¶

Jafnan

lýsir ferli í planinu sem er hringur með miðju í (0,0) og geisla 1. Dæmi um ólíkar stikanir:

1.4.1. Skilgreining¶

Stikaferill \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}\) er diffranlegur í punkti \(t\) ef markgildið

er til. Stikaferillinn \(\mbox{${\bf r}$}\) er sagður diffranlegur ef hann er diffranlegur í öllum punktum á bilinu \([a,b]\). (Í endapunktum bilsins \([a,b]\) er þess krafist að einhliða afleiður séu skilgreindar.)

1.4.2. Setning¶

Stikaferill \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}\) er diffranlegur í punkti \(t\) ef og aðeins ef föllin \(r_1,\ldots,r_n\) eru öll diffranleg í \(t\). Þá gildir að

1.4.3. Ritháttur¶

Látum \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}\) vera diffranlegan stikaferil. Venja er að rita \(\mbox{${\bf v}$}(t)=\mbox{${\bf r}$}'(t)\) og tala um \(\mbox{${\bf v}$}(t)\) sem hraðaen: velocity.
Smelltu fyrir ítarlegri þýðingu. eða hraðavigur. Talan \(|\mbox{${\bf v}$}(t)|\) er kölluð ferðEkki fannst þýðing á hugtakinu: ferð. Einnig er ritað \(\mbox{${\bf a}$}(t)=\mbox{${\bf v}$}'(t)=\mbox{${\bf r}$}''(t)\) og talað um \(\mbox{${\bf a}$}(t)\) sem hröðunen: acceleration.
Smelltu fyrir ítarlegri þýðingu. eða hröðunarvigur.

1.4.4. Dæmi¶

Lítum á eftirfarand stikaferla sem stika hring með miðju í (0,0) og geisla 1.

Þá er tilsvarandi hraði

og ferðin \(|\mbox{${\bf v}$}_1(t)| = 1\) og \(|\mbox{${\bf v}$}_2(t)| = 2t\).

1.4.5. Setning¶

Látum \(\mbox{${\bf u}$},\mbox{${\bf v}$}:[a,b]\rightarrow \mbox{${\bf R}^n$}\) vera diffranlega stikaferla og \(\lambda\) diffranlegt fall. Þá eru stikaferlarnir \(\mbox{${\bf u}$}(t)+\mbox{${\bf v}$}(t), \lambda(t)\mbox{${\bf u}$}(t)\) og \(\mbox{${\bf u}$}(\lambda(t))\) diffranlegir, og ef \(n=3\) þá er stikaferillinn \(\mbox{${\bf u}$}(t)\times \mbox{${\bf v}$}(t)\) líka diffranlegur. Fallið \(\mbox{${\bf u}$}(t)\cdot\mbox{${\bf v}$}(t)\) er líka diffranlegt. Eftirfarandi listi sýnir formúlur fyrir afleiðunum:

(a) \(\frac{d}{dt}(\mbox{${\bf u}$}(t)+\mbox{${\bf v}$}(t))=\mbox{${\bf u}$}'(t)+\mbox{${\bf v}$}'(t)\),

(b) \(\frac{d}{dt}(\lambda(t)\mbox{${\bf u}$}(t))=\lambda'(t)\mbox{${\bf u}$}(t)+\lambda(t)\mbox{${\bf u}$}'(t)\),

(c) \(\frac{d}{dt}(\mbox{${\bf u}$}(t)\cdot\mbox{${\bf v}$}(t))=\mbox{${\bf u}$}'(t)\cdot\mbox{${\bf v}$}(t)+\mbox{${\bf u}$}(t)\cdot\mbox{${\bf v}$}'(t)\),

(d) \(\frac{d}{dt}(\mbox{${\bf u}$}(t)\times\mbox{${\bf v}$}(t))=\mbox{${\bf u}$}'(t)\times\mbox{${\bf v}$}(t)+\mbox{${\bf u}$}(t)\times\mbox{${\bf v}$}'(t)\),

(e) \(\frac{d}{dt}(\mbox{${\bf u}$}(\lambda(t)))=\mbox{${\bf u}$}'(\lambda(t))\lambda'(t)\).

Ef \(\mbox{${\bf u}$}(t)\neq\mbox{${\bf 0}$}\) þá er

(f) \(\frac{d}{dt}|\mbox{${\bf u}$}(t)|=\frac{\mbox{${\bf u}$}(t)\cdot\mbox{${\bf u}$}'(t)}{|\mbox{${\bf u}$}(t)|}\).

1.4.6. Skilgreining¶

Látum \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}; \mbox{${\bf r}$}(t)=(r_1(t),\ldots,r_n(t))\) vera stikaferil.

Stikaferillinn er sagður samfellt diffranleguren: continuously differentiable.
Smelltu fyrir ítarlegri þýðingu. ef föllin \(r_1(t),\ldots,r_n(t)\) eru öll diffranleg og afleiður þeirra eru samfelldar. Samfellt diffranlegur stikaferill er sagður þjállen: infinitely differentiable.
Smelltu fyrir ítarlegri þýðingu. ef \(\mbox{${\bf r}$}'(t)\neq\mbox{${\bf 0}$}\) fyrir öll \(t\).

Stikaferillinn er sagður samfellt diffranlegur á köflum ef til eru tölur \(b_0,\ldots,b_k\) þannig að \(a=b_0<b_1<\cdots<b_k=b\) og stikaferillinn er samfellt diffranlegur á hverju bili \([b_{i-1}, b_i]\). Það að stikaferill sé þjáll á köflumen: piecewise smooth.
Smelltu fyrir ítarlegri þýðingu. er skilgreint á sambærilegan hátt.

1.4.7. Setning¶

Látum \(\mbox{${\bf r}$}=f(t)\mbox{${\bf i}$}+g(t)\mbox{${\bf j}$}\) vera samfellt diffranlegan stikaferil fyrir \(t\) á bili \(I\). Ef \(f'(t) \neq 0\) á \(I\) þá hefur ferilinn snertilínuen: tangent.
Smelltu fyrir ítarlegri þýðingu. fyrir hvert gildi á \(t\) og hallatala hennar er

Ef \(g'(t) \neq 0\) á \(I\) þá hefur ferilinn þverlínuen: normal.
Smelltu fyrir ítarlegri þýðingu. fyrir hvert gildi á \(t\) og hallatala hennar er

1.5.1. Regla¶

Látum \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}\) vera samfellt diffranlegan stikaferil. Lengd eða bogalengden: arc length.
Smelltu fyrir ítarlegri þýðingu. stikaferilsins er skilgreind með formúlunni

1.5.2. Skilgreining og umræða¶

Látum \(\mbox{${\bf r}$}: [a,b]\rightarrow \mbox{${\bf R}^n$}\) vera samfellt diffranlegan stikaferil. Sagt er að stikaferillinn sé stikaður með bogalengd ef fyrir allar tölur \(t_1, t_2\) þannig að \(a\leq t_1<t_2\leq b\) þá gildir

(Skilyrðið segir að lengd stikaferilsins á milli punkta \(\mbox{${\bf r}$}(t_1)\) og \(\mbox{${\bf r}$}(t_2)\) sé jöfn muninum á \(t_2\) og \(t_1\).) Stikun með bogalengd má líka þekkja á þeim eiginleika að \(|\mbox{${\bf v}$}(t)|=1\) fyrir öll gildi á \(t\).

Sýnidæmi

Stikum gormferilinn \({\bf r} = a \cos(t) {\bf i} + a \sin(t) {\bf j} + b t {\bf k}\) með bogalengd frá punkti \((a,0,0)\) í stefnu vaxandi \(t\).

Lausn: Reiknum

\[\begin{split}\begin {aligned} \mathbf{v}(t) &= -a \sin(t)\mathbf{i} + a \cos(t) \mathbf{j} \quad \text{og} \\ |\mathbf{v}(t)| &= \sqrt{a^2(\sin^2(t)+\cos^2(t))+b^2}= \sqrt{a^2+b^2}. \end{aligned}\end{split}\]

Þá er lengd ferilsins frá \(0\) til \(t\) gefin með

\[s(t) = \int_0^t \sqrt{a^2+b^2} d\tau = \sqrt{a^2+b^2}t\]

og ef við leysum fyrir \(t\) sem fall af \(s\) fæst

\[t = \frac{s}{\sqrt{a^2+b^2}}.\]

Þá er stikun með bogalengd, köllum hana \(\mathbf{r}_b\), gefin með

\[\mathbf{r}_b(s) = \mathbf{r}(t(s)) = a \cos\left(\frac{s}{\sqrt{a^2+b^2}}\right)\mathbf{i} + a \sin\left(\frac{s}{\sqrt{a^2+b^2}}\right)\mathbf{j} + \frac{bs}{\sqrt{a^2+b^2}}\mathbf{k}.\]

Gormferillinn fyrir gildin \(a=b=1\) og \(\theta \in [0,4\pi]\).

1.6.1. Skilgreining¶

Látum \(P=(x,y)\neq \mbox{${\bf 0}$}\) vera punkt í plani. Pólhniten: polar coordinates.
Smelltu fyrir ítarlegri þýðingu. \(P\) er talnapar \([r,\theta]\) þannig að \(r\) er fjarlægð \(P\) frá \(O=(0,0)\) og \(\theta\) er hornið á milli striksins \(\overline{OP}\) og \(x\)-ássins. (Hornið er mælt þannig að rangsælis stefna telst jákvæð, og leggja má við \(\theta\) heil margfeldi af \(2\pi\).)

1.6.2. Regla¶

Ef pólhnit punkts í plani eru \([r, \theta]\) þá má reikna hornrétt hniten: orthogonal coordinates.
Smelltu fyrir ítarlegri þýðingu. hans (\(xy\)-hnit) með formúlunum

Ef við þekkjum \(xy\)-hnit punkts þá má finna pólhnitin út frá jöfnunum

(Ef \(x=0\) þá má taka \(\theta=\frac{\pi}{2}\) ef \(y>0\) en \(\theta=-\frac{\pi}{2}\) ef \(y<0\). Þegar jafnan \(\tan\theta=\frac{y}{x}\) er notuð til að ákvarða \(\theta\) þá er tekin lausn á milli \(-\frac{\pi}{2}\) og \(\frac{\pi}{2}\) ef \(x>0\) en á milli \(\frac{\pi}{2}\) og \(\frac{3\pi}{2}\) ef \(x<0\).)

1.7.1. Skilgreining og umræða¶

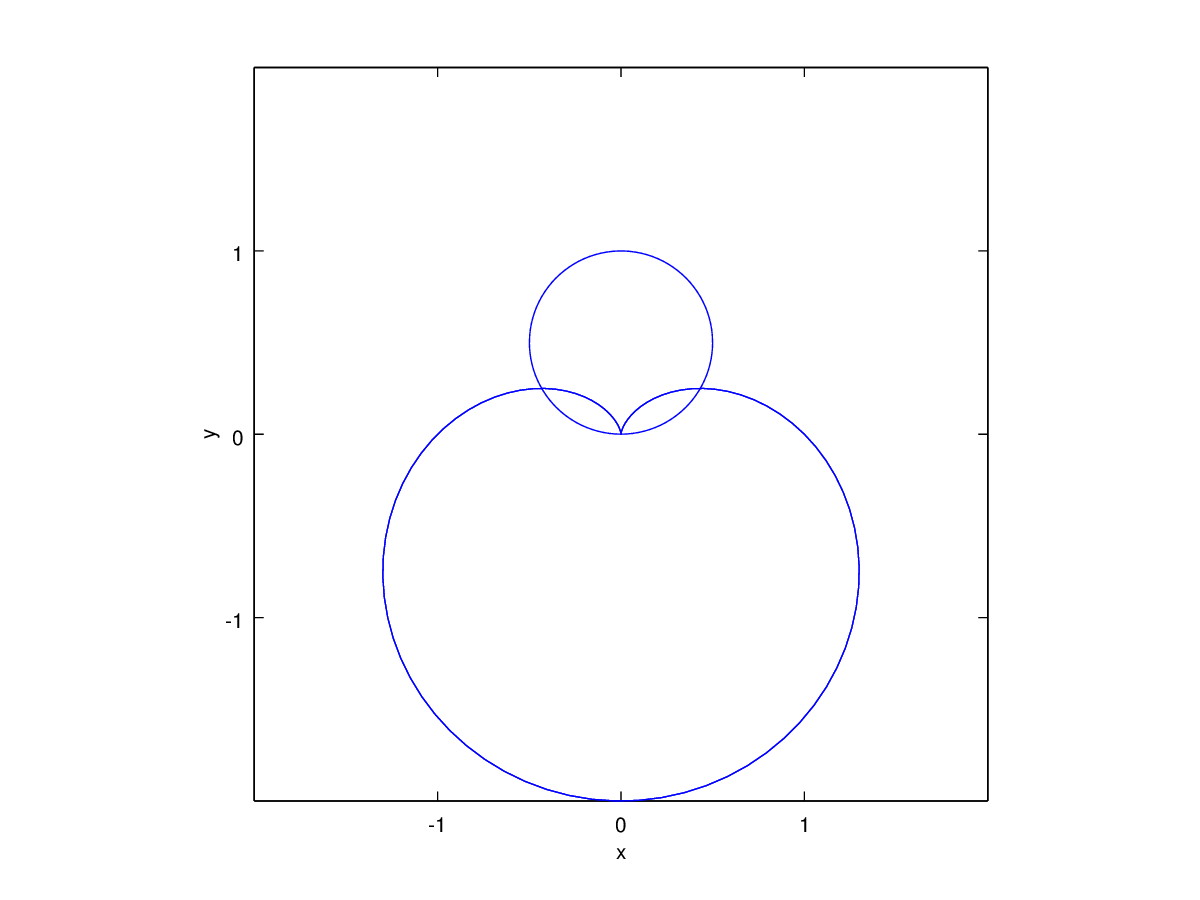
Látum \(f\) vera fall skilgreint fyrir \(\theta\) þannig að \(\alpha\leq\theta\leq\beta\). Jafnan \(r=f(\theta)\) lýsir mengi allra punkta í planinu sem hafa pólhnit á forminu \([f(\theta),\theta]\) þar sem \(\alpha\leq\theta\leq\beta\). Þetta mengi kallast pólhnitagraf fallsins \(f\).

Pólhnitagraf er ferill í planinu sem má stika með stikaferlinum

með formúlu

Sýnidæmi

Finnum skurðpunkta hjartaferilsins \(r = 1-\sin\theta\) og hringsins \(r=\sin\theta\).

Lausn: Athugum fyrst hvort ferlarnir skerist fyrir sama gildi á \(r>0\) og \(\theta\). Leysum þá jöfnuna \(1-\sin\theta = \sin\theta\) og fáum \(\sin\theta = \frac{1}{2}\). Hjartaferillinn er með lotu \(2\pi\) en hringurinn lotu \(\pi\) svo nóg er að skoða lausnir fyrir \(\theta \in [0,2\pi]\). Fáum lausnir \(\theta = \pi/6\) og \(\theta = 5\pi/6\) og skurðpunktarnir eru því \([1/2,\pi/6]\) og \([1/2,5\pi/6]\).

Athugið að við þurfum einnig að athuga hvort ferlarnir skerist þegar \(r=0\) en þá gætu þeir skorist fyrir ólík gildi á \(\theta\). Hjartaferillinn sker punktinn \((0,0)\) þegar \(\theta = \pi/2\) og hringurinn sker \((0,0)\) fyrir \(\theta=0\) og því er \((0,0)\) einnig skurðpunktur.

Hringurinn og hjartaferillinn saman á mynd. Á myndinni má sjá skurðpunktana þrjá sem reiknaðir voru að ofan.

1.9. Flatarmál¶

1.9.1. Setning¶

Flatarmálen: area.
Smelltu fyrir ítarlegri þýðingu. svæðisins sem afmarkast af geislunum \(\theta=\alpha\) og \(\theta=\beta\) (með \(\alpha\leq \beta\) og \(\beta-\alpha\leq 2\pi\)) og pólhnitagrafi \(r=f(\theta)\) (\(f\) samfellt) er

\[\displaystyle\]\[A=\frac{1}{2}\int_\alpha^\beta r^2\,d\theta =\frac{1}{2}\int_\alpha^\beta f(\theta)^2\,d\theta.\]

Sýnidæmi

Finnum flatarmál svæðisins sem afmarkast af spíralnum \(r=\theta\) og geislunum \(\theta = 0\) og \(\theta = 2\pi\).

Lausn: Köllum flatarmálið \(A\). Reiknum

\[A = \frac{1}{2} \int_0^{2\pi} \theta^2 d\theta = \frac{1}{2}\frac{1}{3}(2\pi)^3 = \frac{4\pi^3}{3}.\]

Mynd af spíralnum (í bláu) og geislunum (í rauðu). Svæðið afmarkast af bláu og rauðu ferlunum.

1.13. Meginþverill¶

1.13.1. Skilgreining¶

Látum \(\cal C\) vera feril í plani eða rúmi og \(\mbox{${\bf r}$}\) stikun á \(\cal C\) með bogalengd. Meginþverillen: first normal.
Smelltu fyrir ítarlegri þýðingu. í punkti \(\mbox{${\bf r}$}(s)\) er skilgreindur sem vigurinn

\[\displaystyle \mbox{${\bf N}$}(s)=\frac{\mbox{${\bf T}$}'(s)}{|\mbox{${\bf T}$}'(s)|}=\frac{1}{\kappa(s)}\mbox{${\bf T}$}'(s).\]

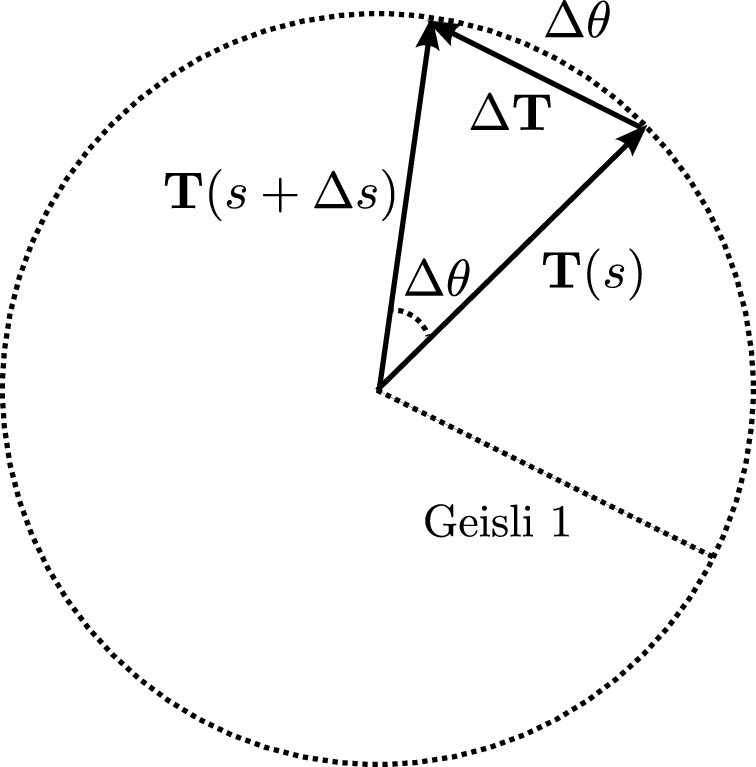
1.13.2. Umræða¶

Táknum með \(\theta\) hornið sem \(\mbox{${\bf T}$}\) myndar við grunnvigurinn \(\mbox{${\bf i}$}\). Þá er \(\kappa = \frac{d\theta}{ds}\).