2. Hlutafleiður¶

“If you need help bark like a dog.“ - Gendry. „That’s stupid. If I need help I’ll shout help.“ - Arya”

- George R.R. Martin, A Clash of Kings

2.1. Graf falls¶

2.1.1. Skilgreining¶

Látum $f:{\mathbb R}^2\rightarrow {\mathbb R}$ vera fall. Graf fallsins er skilgreint sem mengið

\[\displaystyle \{(x,y,f(x,y))\mid (x,y)\in{\mathbb R}^2\}\subseteq {\mathbb R}^3.\]

Ef $f:{\mathbb R}^3\rightarrow {\mathbb R}$ er fall, þá er graf fallsins skilgreint sem mengið

\[\displaystyle \{(x,y,z,f(x,y,z))\mid (x,y,z)\in{\mathbb R}^3\}\subseteq {\mathbb R}^4.\]

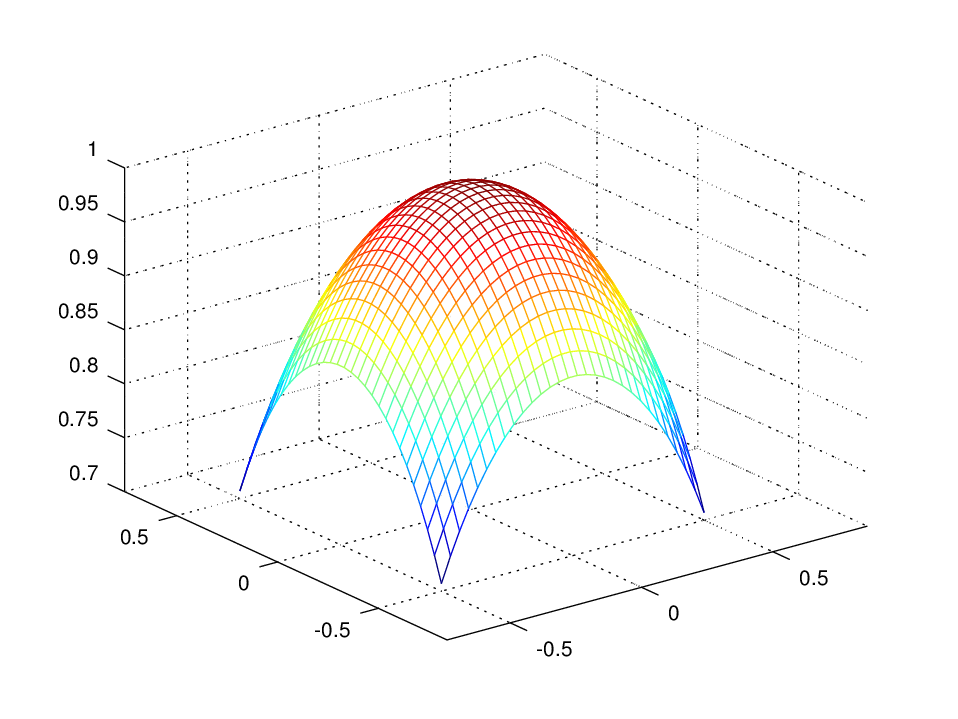
Graf fallsins $f(x,y) = \sqrt{1-x^2-y^2}$, $-0.5\leq x,y\leq 0.5$.

2.2. Jafnhæðarlínur¶

2.2.1. Skilgreining¶

Látum $f:{\mathbb R}^2\rightarrow {\mathbb R}$ vera fall. Ef $c$ er fasti þá er mengið

\[\displaystyle \{(x,y)\mid f(x,y)=c\}\subseteq {\mathbb R}^2\]

kallað jafnhæðarlínaen: contour line.
Smelltu fyrir ítarlegri þýðingu. eða jafnhæðarferillen: contour line.
Smelltu fyrir ítarlegri þýðingu. fallsins $f$ fyrir fastann $c$.

Látum $f:{\mathbb R}^3\rightarrow {\mathbb R}$ vera fall. Ef $c$ er fasti þá er mengið

\[\displaystyle \{(x,y,z)\mid f(x,y,z)=c\}\]

kallað jafnhæðarflöturen: contour surface.
Smelltu fyrir ítarlegri þýðingu. fallsins $f$ fyrir fastann $c$.

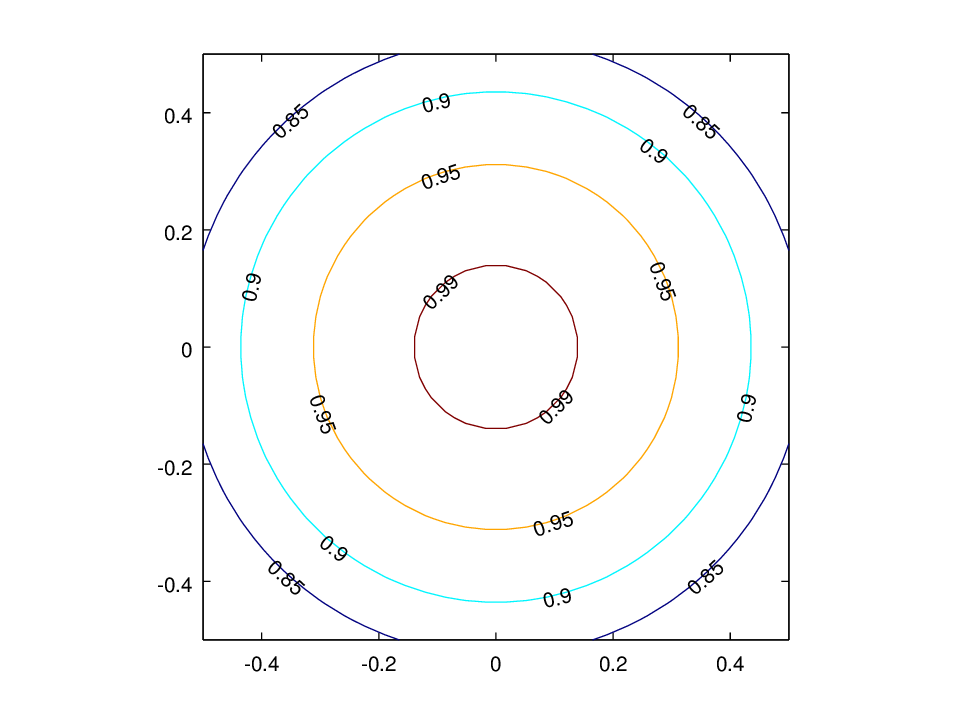
Nokkrar jafnæðarlínur fallsins $f(x,y) = \sqrt{1-x^2-y^2}$, $-0.5\leq x,y\leq 0.5$.

2.3. Fjarlægð milli punkta¶

2.3.1. Skilgreining¶

Fjarlægðin milli tveggja punkta $\mbox{${\bf x}$}=(x_1,x_2, \ldots,x_n)$ og $\mbox{${\bf y}$}=(y_1,y_2, \ldots,y_n)$ í $\mbox{${\bf R}^n$}$ er skilgreind sem talan

\[\displaystyle |\mbox{${\bf x}$}-\mbox{${\bf y}$}|=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2}.\]

2.4. Opnar kúlur¶

2.4.1. Skilgreining¶

Látum $P=(p_1,p_2,\ldots,p_n)$ vera punkt í $\mbox{${\bf R}^n$}$. Skilgreinum opnu kúluna með miðju í $P$ og geisla $r$ sem mengið

\[\displaystyle B_r(P)=\{Q\in\mbox{${\bf R}^n$}\mid |Q-P|<r\}.\]

Í ${\mathbb R}^2$ er eðlilegra að tala um opna skífu eða opinn disk í stað opinnar kúlu og í ${\mathbb R}$ þá er talað um opin bil.

2.5. Opin mengi¶

2.5.1. Skilgreining¶

Látum $U$ vera hlutmengi í $\mbox{${\bf R}^n$}$.

Sagt er að $U$ sé opið mengien: open set.
Smelltu fyrir ítarlegri þýðingu. ef um sérhvern punkt $P$ í $U$ gildir að til er tala $r>0$ þannig að $B_r(P)\subseteq U$.

Mengið $U$ er sagt lokaðen: closed set.
Smelltu fyrir ítarlegri þýðingu. ef fyllimengiðen: complement.
Smelltu fyrir ítarlegri þýðingu. er opið. (Fyllimengi $U$ er skilgreint sem mengið $\mbox{${\bf R}^n$}\setminus U=\{Q\in \mbox{${\bf R}^n$}\mid Q\mbox{$\;\not\in\;$}U\}$.)

2.6. Jaðarpunktur¶

2.6.1. Skilgreining¶

Látum $U$ vera mengi í $\mbox{${\bf R}^n$}$. Punktur $P$ í $\mbox{${\bf R}^n$}$ er sagður jaðarpunkturen: boundary point.
Smelltu fyrir ítarlegri þýðingu. $U$ ef sérhver opin kúla $B_r(P)$ með $r>0$ inniheldur bæði punkt úr $U$ og punkt úr $\mbox{${\bf R}^n$}\setminus U$. (Athugið að bæði er mögulegt að jaðarpunktur $U$ sé í $U$ og að hann sé ekki í $U$.)

2.7. Skilgreiningarmengi¶

2.7.1. Skilgreining¶

Fyrir fall $f(x_1,x_2,\ldots,x_n)$ þá táknar ${\cal D}(f)$ skilgreiningarmengien: argument domain.
Smelltu fyrir ítarlegri þýðingu. fallsins $f$. Ef fallið er gefið með formúlu og ekkert sagt um ${\cal D}(f)$ þá lítum við svo á að ${\cal D}(f)$ sé mengi allra punkta í $\mbox{${\bf R}^n$}$ þannig að formúlan gefi vel skilgreinda tölu.

2.8. Markgildi¶

2.8.1. Skilgreining¶

Látum $f(x_1,x_2,\ldots,x_n)$ vera fall af $n$ breytistærðum með skilgreiningarmengi ${\cal D}(f)\subseteq \mbox{${\bf R}^n$}$. Látum $P=(p_1,p_2,\ldots,p_n)$ vera punkt í $\mbox{${\bf R}^n$}$ þannig að sérhver opin kúla um $P$ inniheldur meira en einn punkt úr ${\cal D}(f)$.

Segjum að $f(x_1,x_2,\ldots,x_n)$ stefni áen: converge to.
Smelltu fyrir ítarlegri þýðingu. tölu $L$ þegar $(x_1,x_2,\ldots,x_n)$ stefnir á $(p_1,p_2,\ldots,p_n)$ ef eftirfarandi gildir:

Fyrir sérhverja tölu $\epsilon>0$ er til tala $\delta>0$ þannig að ef $(x_1,x_2,\ldots,x_n)\in{\cal D}(f)$ og

\[ \begin{align}\begin{aligned}\displaystyle\\0<|(x_1,x_2,\ldots,x_n)-(p_1,p_2,\ldots,p_n)|<\delta\end{aligned}\end{align} \]

þá er

\[\displaystyle |f(x_1,x_2,\ldots,x_n)-L|<\epsilon.\]

2.8.2. Ritháttur¶

Ef $f(x_1,x_2,\ldots,x_n)$ stefnir á tölu $L$ þegar $(x_1,x_2,\ldots,x_n)$ stefnir á $(p_1,p_2,\ldots,p_n)$ þá er ritað

\[ \begin{align}\begin{aligned}\displaystyle\\\lim_{(x_1,x_2,\ldots,x_n)\rightarrow (p_1,p_2,\ldots,p_n)} f(x_1,x_2,\ldots,x_n)=L.\end{aligned}\end{align} \]

og $L$ kallast markgildiEkki fannst þýðing á hugtakinu: markgildi fallsins $f$ í punktinum $(x_1,x_2,\ldots,x_n)$.

2.8.3. Skilgreining (Skilgreining 2.8.1 sett fram fyrir föll af tveimur breytum.)¶

Látum $f(x,y)$ vera fall skilgreint á mengi ${\cal D}(f)\subseteq {\mathbb R}^2$. Látum $(a,b)$ vera punkt í ${\mathbb R}^2$ þannig að sérhver opin skífa um $(a,b)$ inniheldur meira en einn punkt úr ${\cal D}(f)$.

Segjum að $f(x,y)$ stefni á tölu $L$ þegar $(x,y)$ stefnir á $(a,b)$ ef eftirfarandi gildir:

Fyrir sérhverja tölu $\epsilon>0$ er til tala $\delta>0$ þannig að ef $(x,y)\in{\cal D}(f)$ og

\[ \begin{align}\begin{aligned}\displaystyle\\\delta > |(x,y)-(a,b)| = \sqrt{(x-a)^2+(y-b)^2} > 0\end{aligned}\end{align} \]

þá er

\[\displaystyle |f(x,y)-L|<\epsilon.\]

2.9. Reglur um markgildi¶

2.9.1. Setning¶

Látum $f$ og $g$ vera föll af tveimur breytum. Gerum ráð fyrir að

\[ \begin{align}\begin{aligned}\displaystyle\\\lim_{(x,y)\rightarrow (a,b)}f(x,y)=L\quad\mbox{og}\quad \lim_{(x,y)\rightarrow (a,b)}g(x,y)=M,\end{aligned}\end{align} \]

og að sérhver grennden: neighbourhood.
Smelltu fyrir ítarlegri þýðingu. um $(a,b)$ innihaldi fleiri en einn punkt þar sem bæði föllin $f$ og $g$ eru skilgreind. Þá gildir

(a) $\lim_{(x,y)\rightarrow (a,b)}(f(x,y)\pm g(x,y))=L\pm M$.

(b) $\lim_{(x,y)\rightarrow (a,b)}f(x,y) g(x,y)=LM$.

(c) $\lim_{(x,y)\rightarrow (a,b)}\frac{f(x,y)}{g(x,y)}= \frac{L}{M}$, svo framarlega sem $M\neq 0$.

(d) $\lim_{(x,y)\rightarrow (a,b)}F(f(x,y))=F(L)$ ef $F$ er fall af einni breytistærð sem er samfellt í punktinum $L$.

2.10. Samfelldni¶

2.10.1. Skilgreining¶

Látum $f$ vera fall af $n$ breytistærðum skilgreint á mengi ${\cal D}(f)$ í $\mbox{${\bf R}^n$}$. Fallið $f$ er sagt samfellt í punkti $(p_1,p_2,\ldots,p_n)$ í ${\cal D}(f)$ ef

\[ \begin{align}\begin{aligned}\displaystyle\\\lim_{(x_1,x_2,\ldots,x_n)\rightarrow (p_1,p_2,\ldots,p_n)} f(x_1,x_2,\ldots,x_n)=f(p_1,p_2,\ldots,p_n).\end{aligned}\end{align} \]

Sagt er að fallið sé samfellten: continuous.
Smelltu fyrir ítarlegri þýðingu. ef það er samfellt í öllum punktum skilgreiningarmengis síns.

2.11. Hlutafleiður¶

2.11.1. Skilgreining¶

Látum $f(x,y)$ vera fall af tveimur breytum $x$ og $y$ sem er skilgreint á opinni skífu með miðju í punktinum $(a,b)$.

Skilgreinum hlutafleiðuEkki fannst þýðing á hugtakinu: hlutafleiða m.t.t. $x$ í $(a,b)$ með

\[\displaystyle f_1(a,b)=\lim_{h\rightarrow 0}\frac{f(a+h,b)-f(a,b)}{h}\]

og hlutafleiðuEkki fannst þýðing á hugtakinu: hlutafleiða m.t.t. $y$ í $(a,b)$ með

\[\displaystyle f_2(a,b)=\lim_{k\rightarrow 0}\frac{f(a,b+k)-f(a,b)}{k}\]

ef markgildin eru til.

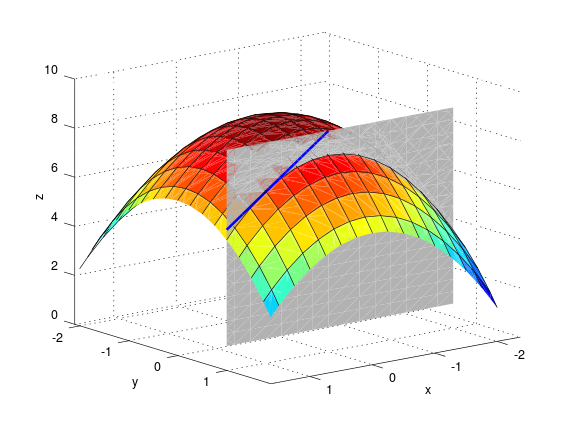
Hlutafleiða m.t.t. $x$ fyrir $y=1$.

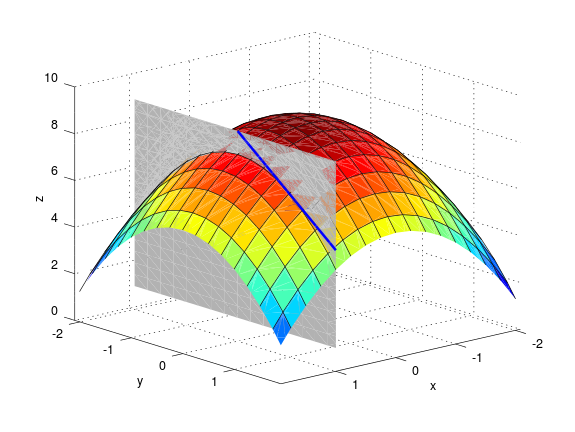
Hlutafleiða m.t.t. $y$ fyrir $x=1$.

2.11.2. Skilgreining¶

Látum $f(x,y,z)$ vera fall af þremur breytum $x$, $y$ og $z$ sem er skilgreint á opinni kúlu með miðju í punktinum $(a, b,c)$.

Skilgreinum hlutafleiðu m.t.t. $x$ í $(a,b,c)$ með

\[\displaystyle f_1(a,b,c)=\lim_{h\rightarrow 0}\frac{f(a+h,b,c)-f(a,b,c)}{h},\]

hlutafleiðu m.t.t. $y$ í $(a,b,c)$ með

\[\displaystyle f_2(a,b,c)=\lim_{k\rightarrow 0}\frac{f(a,b+k,c)-f(a,b,c)}{k}\]

og hlutafleiðu m.t.t. $z$ í $(a,b,c)$ með

\[\displaystyle f_3(a,b,c)=\lim_{\ell\rightarrow 0}\frac{f(a,b,c+\ell)-f(a,b,c)}{\ell}\]

ef markgildin eru til.

2.11.3. Skilgreining¶

Látum $f$ vera fall af $n$ breytum $x_1,x_2,\ldots,x_n$ sem er skilgreint á opinni kúlu um punktinn $\mathbf{a}=(a_1, a_2, \ldots, a_n).$

Hlutafleiða $f$ með tilliti til breytunnar $x_k$ í punktinum $\mathbf{a}$ er skilgreind sem markgildið

\[\displaystyle f_k(\mathbf{a})=\lim_{h\rightarrow 0}\frac{f(\mathbf{a}+h\mbox{${\bf e}$}_k)-f(\mathbf{a})}{h}\]

ef markgildið er til. (Hér stendur $\mbox{${\bf e}$}_k$ fyrir vigurinn sem er með 0 í öllum hnitum nema því $k$-ta þar sem er 1.)

2.11.4. Ritháttur¶

Ritum $z=f(x,y)$. Ýmis konar ritháttur er fyrir hlutafleiður, m.a.

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} f_1(x,y)&=\frac{\partial z}{\partial x}= \frac{\partial }{\partial x}f(x,y) =D_1f(x,y)=f_x(x,y)=D_xf(x,y)=\partial_xf(x,y) \\ f_2(x,y)&=\frac{\partial z}{\partial y}= \frac{\partial }{\partial y}f(x,y) =D_2f(x,y)=f_y(x,y)=D_yf(x,y)=\partial_yf(x,y). \end{aligned}\end{split}\end{aligned}\end{align} \]

Þegar við viljum tákna gildið á hlutafleiðu $f$ í ákveðnum punkti $(x,y)=(a,b)$ þá eru líka ýmsir möguleikar, til dæmis

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} \frac{\partial z}{\partial x}\bigg|_{(a,b)}&= \left(\frac{\partial }{\partial x}f(x,y)\right)\bigg|_{(a,b)} =f_1(a,b)=D_1f(a,b) \\ \frac{\partial z}{\partial y}\bigg|_{(a,b)}&= \left(\frac{\partial }{\partial y}f(x,y)\right)\bigg|_{(a,b)} =f_2(a,b)=D_2f(a,b). \end {aligned}\end{split}\end{aligned}\end{align} \]

Aðvörun

Strangt til tekið merkir rithátturinn $\frac{\partial}{\partial x} f(a,b)$ að við stingum fyrst inn tölunum $a$ og $b$ og diffrum síðan með tilliti til $x$. En þar sem $f(a,b)$ er óháð $x$ er útkoman 0.

2.12. Snertiplan¶

Látum $f(x,y)$ vera fall af tveimur breytistærðum þannig að hlutafleiðurnar $f_1(a,b)$ og $f_2(a,b)$ séu skilgreindar.

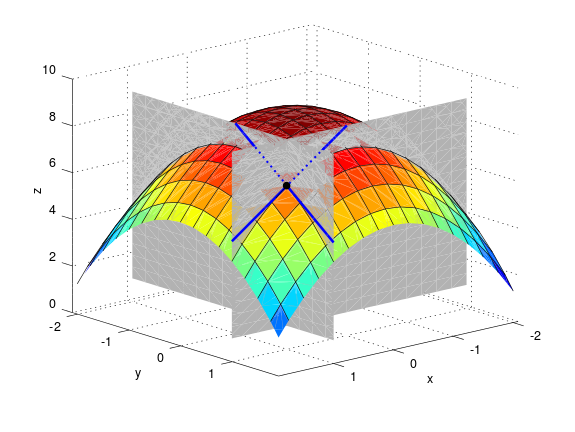
Í punktinum $(a,b,f(a,b))$ er

$\mbox{${\bf T}$}_1 = \mbox{${\bf i}$}+ f_1(a,b)\mbox{${\bf k}$}\qquad$ snertiviguren: tangent vector.
Smelltu fyrir ítarlegri þýðingu. við ferilinn $f(x,b) = z$ og

$\mbox{${\bf T}$}_2 = \mbox{${\bf j}$}+ f_2(a,b)\mbox{${\bf k}$}\qquad$ snertiviguren: tangent vector.
Smelltu fyrir ítarlegri þýðingu. við ferilinn $f(a,y) = z$.

Táknum með $S$ planið sem hefur stikunina

\[\displaystyle (a,b,f(a,b))+s\mbox{${\bf T}$}_1+t\mbox{${\bf T}$}_2, \quad -\infty < s,t < \infty.\]

Vigurinn

\[\displaystyle \mbox{${\bf n}$}=\mbox{${\bf T}$}_2\times \mbox{${\bf T}$}_1=f_1(a,b)\mbox{${\bf i}$}+f_2(a,b)\mbox{${\bf j}$}-\mbox{${\bf k}$}\]

er þvervigur á $S$ og jafna plansins $S$ er

\[\displaystyle z=f(a,b)+f_1(a,b)(x-a)+f_2(a,b)(y-b).\]

Þverlínaen: normal.
Smelltu fyrir ítarlegri þýðingu. á $S$ hefur stikun

\[\displaystyle (a,b,f(a,b)) + u \mbox{${\bf n}$}, \quad -\infty < u < \infty.\]

Ef $f(x,y)$ er ’nógu nálægt’ (skilgreint nánar síðar) planinu $S$ þegar $(x,y)$ er nálægt punktinum $(a,b)$ þá kallast $S$ snertiplanen: tangent plane.
Smelltu fyrir ítarlegri þýðingu. við grafið $z=f(x,y)$ í punktinum $(a,b,f(a,b))$.

2.13. Hlutafleiður af hærra stigi¶

2.13.1. Skilgreining¶

Ritum $z=f(x,y)$. Annars stigs hlutafleiður $f$ eru skilgreindar með formúlunum

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial^2 z}{\partial x^2}= \frac{\partial}{\partial x} \frac{\partial z}{\partial x} =f_{11}(x,y)=f_{xx}(x,y),\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial^2 z}{\partial y^2}= \frac{\partial}{\partial y} \frac{\partial z}{\partial y} =f_{22}(x,y)=f_{yy}(x,y),\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial^2 z}{\partial x\partial y}= \frac{\partial}{\partial x} \frac{\partial z}{\partial y} =f_{21}(x,y)=f_{yx}(x,y),\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial^2 z}{\partial y\partial x}= \frac{\partial}{\partial y} \frac{\partial z}{\partial x} =f_{12}(x,y)=f_{xy}(x,y).\end{aligned}\end{align} \]

Hlutafleiðurnar $f_{11}(x,y)$ og $f_{22}(x,y)$ kallast hreinar hlutafleiður og $f_{12}(x,y)$ og $f_{21}(x,y)$ kallast blandaðar hlutafleiður.

2.13.2. Setning¶

Látum $f(x,y)$ vera fall sem er skilgreint á opinni skífu $D$ með miðju í $P=(a,b)$ . Gerum ráð fyrir að hlutafleiðurnar $f_1(x,y)$, $f_2(x,y)$, $f_{12}(x,y)$ og $f_{21}(x,y)$ séu allar skilgreindar á $D$ og að þær séu allar samfelldar á $D$. Þá gildir að

\[\displaystyle f_{12}(a,b)=f_{21}(a,b).\]

2.13.3. Hugmynd að skilgreiningu¶

Skilgreiningu 5.6 má útvíkka á augljósan hátt til að skilgreina 2. stigs hlutafleiður fyrir föll af fleiri en tveimur breytum. Einnig er augljóst hvernig má skilgreina hlutafleiður af hærri stigum en 2, til dæmis ef $w=f(x,y,z)$ þá

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial^3 w}{\partial x\partial y^2} \quad\quad\mbox{(diffra fyrst tvisvar m.t.t. }y\mbox{, svo einu sinni m.t.t. } x\mbox{)}\end{aligned}\end{align} \]

og

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial^3 w}{\partial y\partial z\partial y} \quad\quad\mbox{(diffra fyrst m.t.t. } y\mbox{, svo m.t.t. } z \mbox{ og að lokum m.t.t. }y\mbox{)}.\end{aligned}\end{align} \]

2.13.4. Setning (Almenn útgáfa af Setningu 2.13.2)¶

Látum $f$ vera fall $n$ breytistærðum sem er skilgreint á opinni kúlu með miðju í $P=(x_1, x_2,\ldots, x_n)$.

Skoðum tvær hlutafleiður $f$ í punktum $P$ þar sem er diffrað með tilliti til sömu breytistærða og jafn oft með tilliti til hverrar breytistærðar. Ef þessar hlutafleiður eru samfelldar í punktinum $P$ og allar hlutafleiður af lægra stigi eru skilgreindar á $D$ og samfelldar á $D$ þá eru hlutafleiðurnar sem við erum að skoða jafnar í $P$.

2.13.5. Dæmi:¶

Ef $w = f(x,y,z)$ er fall af þremur breytistærðum þá er t.d.

\[\displaystyle \frac{\partial^4 w}{\partial x^2\partial y \partial z} = \frac{\partial^4 w}{\partial x \partial y \partial x \partial z}\]

ef skilyrðin í setningunni eru uppfyllt.

2.14. Keðjuregla¶

2.14.1. Setning (Keðjureglan í einni breytistærð.)¶

Við munum nú skoða nokkrar útgáfur af keðjuregluen: chain rule.
Smelltu fyrir ítarlegri þýðingu. fyrir föll af mörgum breytistærðum. Gerum ráð fyrir að fallið $f(u)$ sé diffranlegt í punktinum $u=g(x)$ og að fallið $g(x)$ sé diffranlegt í punktinum $x$. Þá er fallið $(f\circ g)(x)=f(g(x))$ diffranlegt í $x$ og

\[\displaystyle (f\circ g)'(x)=f'(g(x))g'(x).\]

2.14.2. Setning¶

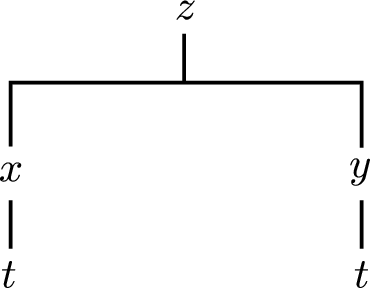
Látum $f(x,y)$ vera fall þar sem $x=x(t)$ og $y=y(t)$ eru föll af breytu $t$. Gerum ráð fyrir að á opinni skífu um punktinum $(x(t),y(t))$ séu báðar fyrsta stigs hlutafleiður $f$ skilgreindar og samfelldar. Gerum enn fremur ráð fyrir að föllin $x(t)$ og $y(t)$ séu bæði diffranleg í punktinum $t$. Þá er fallið

\[\displaystyle g(t)=f(x(t),y(t))\]

diffranlegt í $t$ og

\[\displaystyle g'(t)=f_1(x(t),y(t))x'(t)+f_2(x(t),y(t))y'(t).\]

2.14.3. Ritháttur¶

Ritum $z=f(x,y)$ þar sem $x=x(t)$ og $y=y(t)$ eru föll af breytu $t$. Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt} +\frac{\partial z}{\partial y}\frac{dy}{dt}.\end{aligned}\end{align} \]

2.14.4. Setning¶

Látum $f(x,y)$ vera fall af breytistærðum $x$ og $y$ sem aftur eru föll af breytum $s$ og $t$, það er að segja $x=x(s,t)$ og $y=y(s,t)$. Ritum svo

\[\displaystyle g(s,t)=f(x(s,t),y(s,t)).\]

Þá gildir (að gefnum sambærilegum skilyrðum og í 2.14.2) að

\[ \begin{align}\begin{aligned}\displaystyle g_1(s,t)=f_1(x(s,t),y(s,t))x_1(s,t)+f_2(x(s,t),y(s,t))y_1(s,t),\\og\end{aligned}\end{align} \]

\[\displaystyle g_2(s,t)=f_1(x(s,t),y(s,t))x_2(s,t)+f_2(x(s,t),y(s,t))y_2(s,t).\]

2.14.5. Ritháttur¶

Ritum $z=f(x,y)$ þar sem $x=x(s,t)$ og $y=y(s,t)$ eru föll af breytum $s$ og $t$. Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial z}{\partial s}= \frac{\partial z}{\partial x}\frac{\partial x}{\partial s} +\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}, \quad \text{og}\quad \frac{\partial z}{\partial t}= \frac{\partial z}{\partial x}\frac{\partial x}{\partial t} +\frac{\partial z}{\partial y}\frac{\partial y}{\partial t}.\end{aligned}\end{align} \]

2.14.6. Ritháttur¶

Ritum $z=f(x,y)$ þar sem $x=x(s,t)$ og $y=y(s,t)$ eru föll af breytum $s$ og $t$. Þá er

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{bmatrix}\frac{\partial z}{\partial s} & \frac{\partial z}{\partial t}\end{bmatrix} =\begin{bmatrix}\frac{\partial z}{\partial x} & \frac{\partial z}{\partial y}\end{bmatrix} \begin{bmatrix}\frac{\partial x}{\partial s} & \frac{\partial x}{\partial t}\\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{bmatrix}\end{split}\end{aligned}\end{align} \]

2.14.7. Setning¶

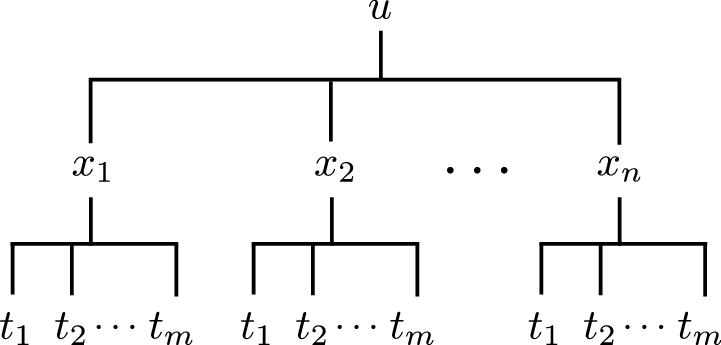
Látum $u$ vera fall af $n$ breytum $x_1, x_2, \ldots, x_n$ þannig að hvert $x_i$ má rita sem fall af $m$ breytum $t_1, t_2, \ldots, t_m$. Gerum ráð fyrir að allar hlutafleiðurnar $\frac{\partial u}{\partial x_i}$ og $\frac{\partial x_i}{\partial t_j}$ séu til og samfelldar. Þegar $u$ er skoðað sem fall af breytunum $t_1, t_2, \ldots, t_m$ fæst að

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial u}{\partial t_j}= \frac{\partial u}{\partial x_1}\frac{\partial x_1}{\partial t_j} +\frac{\partial u}{\partial x_2}\frac{\partial x_2}{\partial t_j} +\cdots+ \frac{\partial u}{\partial x_n}\frac{\partial x_n}{\partial t_j}.\end{aligned}\end{align} \]

2.14.8. Dæmi¶

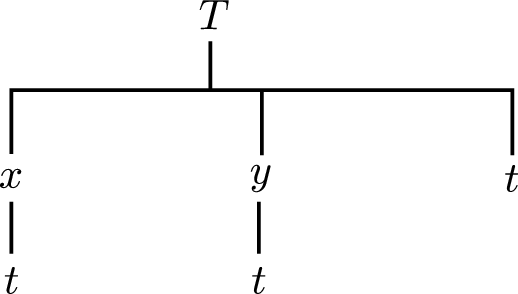
Látum $T$ vera fall af fall af $x$, $y$ og $t$, og $x$ og $y$ föll af $t$. Finnum $\frac{ dT}{dt}$.

\[\displaystyle \frac{d T}{d t} = \frac{\partial T}{\partial x} \frac{d x}{d t} +\frac{\partial T}{\partial y} \frac{d y}{d t} + \frac{\partial T}{\partial t} .\]

2.14.9. Dæmi¶

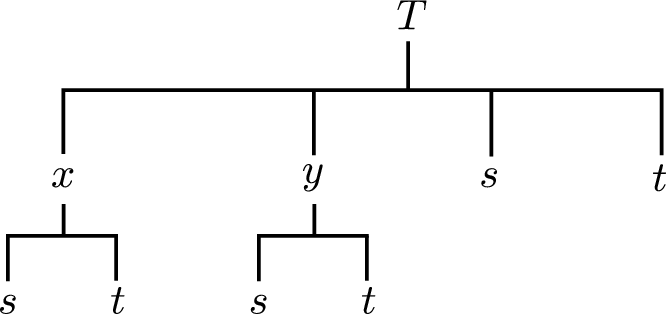
Látum $T$ vera fall af fall af $x$, $y$, $s$ og $t$, og $x$ og $y$ föll af $s$ og $t$. Finnum $\frac{ \partial T}{\partial t}$.

\[\displaystyle \frac{\partial T}{\partial t} = \frac{\partial T}{\partial x} \frac{\partial x}{\partial t} +\frac{\partial T}{\partial y} \frac{\partial y}{\partial t} + \left(\frac{\partial T}{\partial t}\right)_{x,y,s} .\]

2.14.10. Dæmi¶

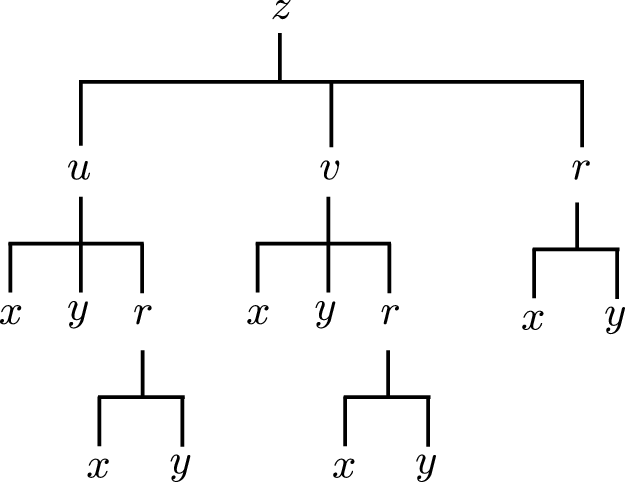
Látum $z$ vera fall af fall af $u$, $v$ og $r$, $u$ og $v$ vera föll af $x$, $y$ og $r$ og $r$ vera fall af $x$ og $y$. Skrifum niður $\frac{\partial z}{\partial x}$.

\[ \begin{align}\begin{aligned}\displaystyle\\\displaystyle\frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} +\frac{\partial z}{\partial u} \frac{\partial u}{\partial r} \frac{\partial r}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial r} \frac{\partial r}{\partial x} +\frac{\partial z}{\partial r} \frac{\partial r}{\partial x}.\end{aligned}\end{align} \]

2.15. Diffranleiki í einni breytistærð¶

2.15.1. Skilgreining¶

Látum $f$ vera fall af einni breytistærð og gerum ráð fyrir að $f$ sé skilgreint á opnu bili sem inniheldur punktinn $a$. Fallið $f$ er sagt vera diffranlegten: differentiable.
Smelltu fyrir ítarlegri þýðingu. í punkti $a$ ef markgildið

\[\displaystyle f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\]

er til.

2.16. Diffranleiki í einni breytistærð - önnur lýsing¶

2.16.1. Skilgreining¶

Látum $f$ vera fall af einni breytistærð og gerum ráð fyrir að $f$ sé skilgreint á opnu bili sem inniheldur punktinn $a$. Fallið $f$ er sagt vera diffranlegten: differentiable.
Smelltu fyrir ítarlegri þýðingu. í punkti $a$ ef til er tala $m$ þannig að ef $L(x)=f(a)+m(x-a)$ þá er

\[\displaystyle \lim_{h\rightarrow 0}\frac{f(a+h)-L(a+h)}{h}=0.\]

(Talan $m$ verður að vera jöfn $f'(a)$.)

Fallið $f$ er ’nálægt’ línunni $L$ nálægt punktinum $a$.

2.17. Diffranleiki¶

2.17.1. Skilgreining¶

Fall $f(x,y)$ sem er skilgreint á opinni skífu umhverfis $(a,b)$ er sagt vera diffranlegten: differentiable.
Smelltu fyrir ítarlegri þýðingu. í punktinum $(a,b)$ ef báðar fyrsta stigs hlutafleiður $f$ eru skilgreindar í $(a,b)$ og ef

\[ \begin{align}\begin{aligned}\displaystyle\\\lim_{(h,k)\rightarrow (0,0)} \frac{f(a+h, b+k)-S(a+h,b+k)}{\sqrt{h^2+k^2}}=0\end{aligned}\end{align} \]

þar sem $S(x,y) = f(a,b) + f_1(a,b)(x-a)+f_2(a,b)(y-b)$.

Fallið $f$ er ’nálægt’ sléttunni $S$ nálægt punktinum $(a,b)$.

2.18. Snertiplan¶

Ef $f$ er diffranlegt í $(a,b)$ þá kallast planið $S$ snertiplanen: tangent plane.
Smelltu fyrir ítarlegri þýðingu. við graf fallsins.

$S(x,y) = f(a,b) + f_1(a,b)(x-a)+f_2(a,b)(y-b)$.

2.19. Diffranleiki¶

2.19.1. Setning (Meðalgildissetningin)¶

Gerum ráð fyrir að fallið $f$ sé samfellt á lokaða bilinu $[a,b]$ og diffranlegt á opna bilinu $(a,b)$. Þá er til punktur $c$ á opna bilinu $(a,b)$ þannig að

\[\displaystyle f(b)-f(a)=f'(c)(b-a).\]

2.19.2. Setning¶

Látum $f(x,y)$ vera fall sem er skilgreint á opinni skífu $\cal D$ með miðju í $(a,b)$ þannig að á þessari skífu eru báðar fyrsta stigs hlutafleiður $f$ skilgreindar og samfelldar. Gerum ráð fyrir að $h$ og $k$ séu tölur þannig að $(x+h, y+k)\in{\cal D}$. Þá eru til tölur $\theta_1$ og $\theta_2$ á milli 0 og 1 þannig að

\[\displaystyle f(a+h,b+k)-f(a,b)=hf_1(a+\theta_1h,b+k)+kf_2(a,b+\theta_2k).\]

2.19.3. Setning¶

Látum $f(x,y)$ vera fall sem er skilgreint á opinni skífu $\cal D$ með miðju í $(a,b)$ þannig að á þessari skífu eru báðar fyrsta stigs hlutafleiður $f$ skilgreindar og samfelldar. Þá er fallið $f$ diffranlegt í $(a,b)$.

2.19.4. Setning¶

Gerum ráð fyrir að $f(x,y)$ sé fall sem er diffranlegt í punktinum $(a,b)$. Þá er $f$ samfellt í $(a,b)$.

2.19.5. Keðjuregla¶

Ritum $z=f(x,y)$ þar sem $x=x(s,t)$ og $y=y(s,t)$. Gerum ráð fyrir að

$x(a,b)=p$ og $y(a,b)=q$;
fyrsta stigs hlutafleiður $x(s,t)$ og $y(s,t)$ eru skilgreindar í punktinum $(a,b)$;
fallið $f$ er diffranlegt í punktinum $(p,q)$.

Þá eru fyrsta stigs hlutafleiður $z$ með tilliti til breytanna $s$ og $t$ skilgreindar í punktinum $(a,b)$ og um þær gildir að

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial z}{\partial s}= \frac{\partial z}{\partial x}\frac{\partial x}{\partial s} +\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\end{aligned}\end{align} \]

og

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial z}{\partial t}= \frac{\partial z}{\partial x}\frac{\partial x}{\partial t} +\frac{\partial z}{\partial y}\frac{\partial y}{\partial t}.\end{aligned}\end{align} \]

2.20. Diffur¶

2.20.1. Skilgreining¶

Ritum $z=f(x_1, x_2, \ldots, x_n)$. Diffriðen: differential.
Smelltu fyrir ítarlegri þýðingu. af $z$ er skilgreint sem

\[ \begin{align}\begin{aligned}\displaystyle\\dz=df=\frac{\partial z}{\partial x_1}dx_1 +\frac{\partial z}{\partial x_2}dx_2 +\cdots+\frac{\partial z}{\partial x_n}dx_n.\end{aligned}\end{align} \]

Diffrið er nálgun á

\[ \begin{align}\begin{aligned}\displaystyle\\\Delta f=f(x_1+dx_1, x_2+dx_2,\ldots, x_n+dx_n)-f(x_1,x_2,\ldots,x_n).\end{aligned}\end{align} \]

2.21. Varpanir $\mbox{${\bf R}^n$}\rightarrow\mbox{${\bf R}^m$}$¶

2.21.1. Táknmál¶

Látum $\mbox{${\bf f}$}:\mbox{${\bf R}^n$}\rightarrow\mbox{${\bf R}^m$}$ tákna vörpun. Ritum $\mbox{${\bf f}$}=(f_1,\ldots,f_m)$ þar sem hvert $f_i$ er fall $\mbox{${\bf R}^n$}\rightarrow{\mathbb R}$. Fyrir punkt í $\mbox{${\bf R}^n$}$ ritum við $\mbox{${\bf x}$}=(x_1,x_2,\ldots,x_n)$. Síðan ritum við $\mbox{${\bf y}$}=\mbox{${\bf f}$}(\mbox{${\bf x}$})$ þar sem $\mbox{${\bf y}$}=(y_1,y_2,\ldots,y_m)$ og

2.22. Jacobi-fylki¶

2.22.1. Skilgreining¶

Notum táknmálið úr 2.22.1. Ef allar hlutafleiðurnar $\partial y_i/\partial x_j$ eru skilgreindar í punktinum $\mbox{${\bf x}$}$ þá skilgreinum við Jacobi-fylki $f$ í punktinum $\mbox{${\bf x}$}$ sem $m\times n$ fylkið

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}D\mbox{${\bf f}$}(\mbox{${\bf x}$})=\begin{bmatrix} \frac{\partial y_1}{\partial x_1}&\frac{\partial y_1}{\partial x_2}& \cdots&\frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1}&\frac{\partial y_2}{\partial x_2}& \cdots&\frac{\partial y_2}{\partial x_n}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial y_m}{\partial x_1}&\frac{\partial y_m}{\partial x_2}& \cdots&\frac{\partial y_m}{\partial x_n} \end{bmatrix}\end{split}\end{aligned}\end{align} \]

2.23. Diffranleiki varpana $\mbox{${\bf R}^n$}\rightarrow\mbox{${\bf R}^m$}$¶

2.23.1. Skilgreining¶

Notum táknmálið úr 2.22.1 og 2.23.1. Látum $\mbox{${\bf a}$}=(a_1, a_2, \ldots, a_n)$ vera fastan punkt í $\mbox{${\bf R}^n$}$ og ritum $\mbox{${\bf h}$}=(h_1,h_2,\ldots,h_n)$. Vörpunin $\mbox{${\bf f}$}$ er sögð diffranleg í punktinum $\mbox{${\bf a}$}$ ef

\[ \begin{align}\begin{aligned}\displaystyle\\\lim_{\mbox{${\bf h}$}\rightarrow \mbox{${\bf 0}$}}\frac{|\mbox{${\bf f}$}(\mbox{${\bf a}$}+\mbox{${\bf h}$})-\mbox{${\bf f}$}(\mbox{${\bf a}$})-D\mbox{${\bf f}$}(\mbox{${\bf a}$})\mbox{${\bf h}$}|}{|\mbox{${\bf h}$}|}=0.\end{aligned}\end{align} \]

Vörpunin $f$ er ’nálægt’ línulegu vörpuninni $D\mbox{${\bf f}$}$ nálægt punktinum $\mbox{${\bf a}$}$.

Línulega vörpunin $D\mbox{${\bf f}$}$ kallast afleiða $\mbox{${\bf f}$}$.

2.24. Keðjuregla¶

2.24.1. Setning¶

Látum $\mbox{${\bf f}$}:\mbox{${\bf R}^n$}\rightarrow \mbox{${\bf R}^m$}$ og $\mbox{${\bf g}$}:\mbox{${\bf R}^m$}\rightarrow \mbox{${\bf R}^k$}$ vera varpanir. Gerum ráð fyrir að vörpunin $\mbox{${\bf f}$}$ sé diffranleg í punkti $\mbox{${\bf x}$}$ og vörpunin $\mbox{${\bf g}$}$ sé diffranleg í punktinum $\mbox{${\bf y}$}=\mbox{${\bf f}$}(\mbox{${\bf x}$})$. Þá er samskeytta vörpunin $\mbox{${\bf g}$}\circ\mbox{${\bf f}$}:\mbox{${\bf R}^n$}\rightarrow\mbox{${\bf R}^k$}$ diffranleg í $\mbox{${\bf x}$}$ og

\[\displaystyle D(\mbox{${\bf g}$}\circ\mbox{${\bf f}$})(\mbox{${\bf x}$})=D\mbox{${\bf g}$}(\mbox{${\bf f}$}(\mbox{${\bf x}$}))D\mbox{${\bf f}$}(\mbox{${\bf x}$}).\]

2.25. Stigull¶

2.25.1. Skilgreining¶

Látum $f(x,y)$ vera fall og $(x,y)$ punkt þar sem báðar fyrsta stigs hlutafleiður $f$ eru skilgreindar. Skilgreinum stigulen: gradient.
Smelltu fyrir ítarlegri þýðingu. $f$ í punktinum $(x,y)$ sem vigurinn

\[\displaystyle \nabla f(x,y)=f_1(x,y)\mbox{${\bf i}$}+f_2(x,y)\mbox{${\bf j}$}.\]

Stigullen: gradient.
Smelltu fyrir ítarlegri þýðingu. $f$ er stundum táknaður með grad$\,f$.

2.25.2. Ritháttur¶

Oft hentugt að rita

\[\displaystyle \nabla=\mbox{${\bf i}$}\frac{\partial}{\partial x}+ \mbox{${\bf j}$}\frac{\partial}{\partial y}.\]

Þá er litið svo á að $\nabla$ sé diffurvirkien: differential operator.
Smelltu fyrir ítarlegri þýðingu., þ.e.a.s. $\nabla$ gefur fyrirmæli um hvað á að gera við $f$ til að fá $\nabla f(x,y)$.

2.26. Dæmi¶

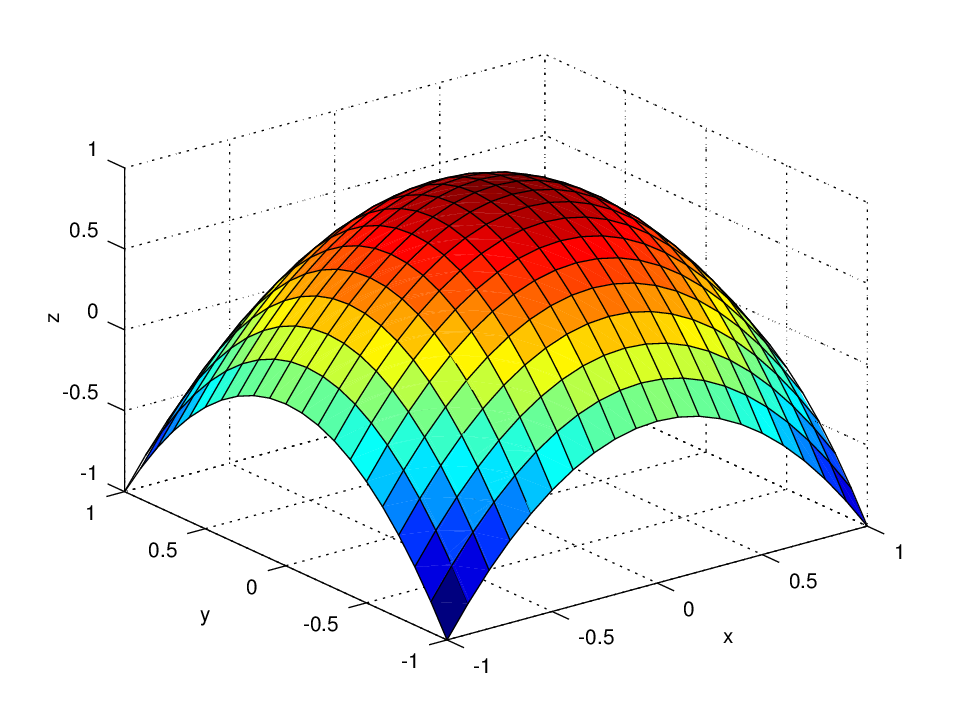
Graf $z=1-x^2-y^2$

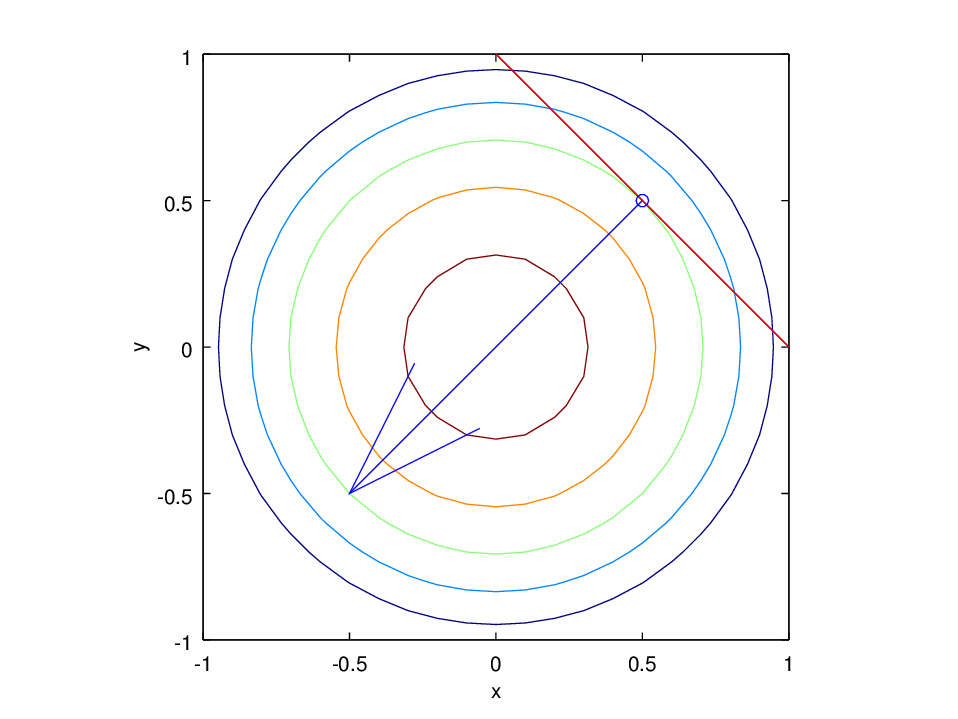
Jafnhæðarlínur $z=1-x^2-y^2$. Stigull og snertilína við jafnhæðarlínuna $z=0.5$ í $(x,y) = (0.5,0.5)$.

2.26.1. Setning¶

Gerum ráð fyrir að fallið $f(x,y)$ sé diffranlegt í punktinum $(a,b)$ og að $\nabla f(a,b) \neq \mathbf{0}$. Þá er vigurinn $\nabla f(a,b)$ hornréttur á þá jafnhæðarlínu $f$ sem liggur í gegnum punktinn $(a,b)$.

2.27. Snertilína við jafnhæðarferil¶

2.27.1. Setning¶

Gerum ráð fyrir að fallið $f(x,y)$ sé diffranlegt í punktinum $(a,b)$ og að $\nabla f(a,b) \neq \mathbf{0}$. Jafna snertilínuen: tangent.
Smelltu fyrir ítarlegri þýðingu. við jafnhæðarferilen: contour line.
Smelltu fyrir ítarlegri þýðingu. $f$ í punktinum $(a,b)$ er gefin með formúlunni

\[\displaystyle \nabla f(a,b)\cdot (x,y)=\nabla f(a,b)\cdot (a,b),\]

eða

\[\displaystyle f_1(a,b)(x-a)+f_2(a,b)(y-b)=0.\]

2.28. Stefnuafleiða¶

2.28.1. Skilgreining¶

Látum $\mbox{${\bf u}$}=u\mbox{${\bf i}$}+v\mbox{${\bf j}$}$ vera einingarvigur. StefnuafleiðaEkki fannst þýðing á hugtakinu: Stefnuafleiða $f$ í punktinum $(a,b)$ í stefnu $\mbox{${\bf u}$}$ er skilgreind sem

\[\displaystyle D_{\mbox{${\bf u}$}}f(a,b)=\lim_{h\rightarrow 0^+}\frac{f(a+hu, b+hv)-f(a,b)}{h}\]

ef markgildið er skilgreint.

Aðvörun

Í skilgreiningunni á stefnuafleiðu er tekið einhliða markgildi. Berið það saman við skilgreiningu á hlutafleiðu þar sem markgildið er tvíhliða.

2.28.2. Setning¶

Gerum ráð fyrir að fallið $f$ sé diffranlegt í $(a,b)$ og $\mbox{${\bf u}$}=u\mbox{${\bf i}$}+v\mbox{${\bf j}$}$ sé einingarvigur. Þá er stefnuafleiðan í punktinum $(a,b)$ í stefnu $\mbox{${\bf u}$}$ skilgreind og gefin með formúlunni

\[\displaystyle D_{\mbox{${\bf u}$}}f(a,b)=\mbox{${\bf u}$}\cdot \nabla f(a,b).\]

2.28.3. Setning¶

Látum $f$ vera gefið fall og gerum ráð fyrir að $f$ sé diffranlegt í punktinum $(a,b)$.

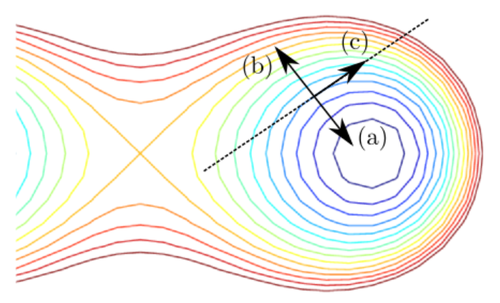
(a) Hæsta gildið á stefnuafleiðunni $D_{\mbox{${\bf u}$}}f(a,b)$ fæst þegar $\mbox{${\bf u}$}$ er einingarvigur í stefnu $\nabla f(a,b)$, þ.e.a.s. $\mbox{${\bf u}$}=\frac{\nabla f(a,b)}{|\nabla f(a,b)|}$.

(b) Lægsta gildið á stefnuafleiðunni $D_{\mbox{${\bf u}$}}f(a,b)$ fæst þegar $\mbox{${\bf u}$}$ er einingarvigur í stefnu $-\nabla f(a,b)$, þ.e.a.s. $\mbox{${\bf u}$}=-\frac{\nabla f(a,b)}{|\nabla f(a,b)|}$.

(c) Ef $\cal C$ er sú hæðarlína $f$ sem liggur í gegnum $(a,b)$ og $\mbox{${\bf u}$}$ er einingarsnertivigur við $\cal C$ í punktinum $(a,b)$ þá er $D_{\mbox{${\bf u}$}}f(a,b)=0$.

2.28.4. Setning¶

Látum $f$ vera gefið fall og gerum ráð fyrir að $f$ sé diffranlegt í punktinum $(a,b)$.

(a) Í punktinum $(a,b)$ þá vex $f$ hraðast ef haldið er í stefnu $\nabla f(a,b)$.

(b) Í punktinum $(a,b)$ þá minnkar $f$ hraðast ef haldið er í stefnu $-\nabla f(a,b)$.

(c) Ef $\cal C$ er sú hæðarlína $f$ sem liggur í gegnum $(a,b)$ og $\mbox{${\bf u}$}$ er einingarsnertivigur við $\cal C$ í punktinum $(a,b)$ þá er er vaxtarhraði $f$ í stefnu $\mbox{${\bf u}$}$ jafn 0.

2.29. Stigull (aftur)¶

2.29.1. Skilgreining¶

Látum $f$ vera fall af þremur breytistærðum, þannig að allar þrjár fyrsta stigs hlutafleiður $f$ í punktinum $(x,y,z)$ séu skilgreindar. Stigullen: gradient.
Smelltu fyrir ítarlegri þýðingu. $f$ í punktinum $(x,y,z)$ er skilgreindur sem vigurinn

\[\displaystyle \nabla f(x,y,z)=f_1(x,y,z)\mbox{${\bf i}$}+f_2(x,y,z)\mbox{${\bf j}$}+f_3(x,y,z)\mbox{${\bf k}$}.\]

2.30. Snertiplan við jafnhæðarflöt¶

2.30.1. Setning¶

Látum $f$ vera fall af þremur breytistærðum þannig að fallið $f$ er diffranlegt í punktinum $(a,b,c)$. Látum $\cal F$ tákna þann jafnhæðarflöten: contour surface.
Smelltu fyrir ítarlegri þýðingu. $f$ sem liggur um $(a,b,c)$. Stigullinn $\nabla f(a,b,c)$ er hornréttur á flötinn $\cal F$ í punktinum $(a,b,c)$ og snertiplanen: tangent plane.
Smelltu fyrir ítarlegri þýðingu. (ef $\nabla f(a,b,c)\neq\mbox{${\bf 0}$}$) við jafnhæðarflötinn í punktinum $(a,b,c)$ er gefið með jöfnunni

\[\displaystyle \nabla f(a,b,c)\cdot(x,y,z)=\nabla f(a,b,c)\cdot(a,b,c)\]

eða með umritun

\[\displaystyle f_1(a,b,c)(x-a)+f_2(a,b,c)(y-b)+f_3(a,b,c)(z-c)=0.\]

2.31. Fólgin föll og Taylor-nálganir¶

2.31.1. Upprifjun¶

Skoðum feril sem gefinn er með jöfnu $F(x,y)=0$ og gerum ráð fyrir að báðar fyrsta stigs hlutafleiður $F$ séu samfelldar. Látum $(x_0,y_0)$ vera punkt á ferlinum. Ef $F_2(x_0,y_0)\neq 0$ þá má skoða $y$ sem fall af $x$ í grennd við punktinn $(x_0,y_0)$ og fallið $y=y(x)$ er diffranlegt í punktinum $x_0$ og afleiðan er gefin með formúlunni

\[\displaystyle y'(x_0)=-\frac{F_1(x_0,y_0)}{F_2(x_0,y_0)}.\]

Sagt að jafnan $F(x,y)=0$ skilgreini $y$ sem fólgið fallen: implicit function.
Smelltu fyrir ítarlegri þýðingu. af $x$ í grennd við $(x_0,y_0)$.

2.31.2. Setning¶

Látum $F$ vera fall af $n$-breytum $x_1, \ldots, x_n$ og gerum ráð fyrir að allar fyrsta stigs hlutafleiður $F$ séu samfelldar. Látum $(a_1,\ldots,a_n)$ vera punkt þannig að $F(a_1,\ldots,a_n)=0$. Ef $F_n(a_1,\ldots,a_n)\neq 0$ þá er til samfellt diffranlegt fall $\varphi(x_1, \ldots, x_{n-1})$ skilgreint á opinni kúlu $B$ utan um $(a_1,\ldots,a_{n-1})$ þannig að

\[\displaystyle \varphi(a_1,\ldots,a_{n-1})=a_n\]

og

\[\displaystyle F(x_1,\ldots, x_{n-1}, \varphi(x_1, \ldots, x_{n-1}))=0\]

fyrir alla punkta $(x_1, \ldots, x_{n-1})$ í $B$.

Ennfremur gildir að

\[ \begin{align}\begin{aligned}\displaystyle\\\varphi_i(a_1,\ldots,a_{n-1}) =-\frac{F_i(a_1,\ldots,a_n)}{F_n(a_1,\ldots,a_n)}.\end{aligned}\end{align} \]

2.31.3. Skilgreining¶

Jacobi-ákveðaEkki fannst þýðing á hugtakinu: Jacobi-ákveða tveggja falla $u=u(x,y)$ og $v=v(x,y)$ með tilliti til breytanna $x$ og $y$ er skilgreind sem

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\frac{\partial(u,v)}{\partial(x,y)}= \begin{vmatrix} \frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x}&\frac{\partial v}{\partial y} \end{vmatrix}.\end{split}\end{aligned}\end{align} \]

Ef $F$ og $G$ eru föll af breytum $x,y,z,\ldots$ þá skilgreinum við, til dæmis,

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\frac{\partial(F,G)}{\partial(x,y)}= \begin{vmatrix} \frac{\partial F}{\partial x}&\frac{\partial F}{\partial y}\\ \frac{\partial G}{\partial x}&\frac{\partial G}{\partial y} \end{vmatrix}\quad \mbox{og}\quad \frac{\partial(F,G)}{\partial(y,z)}= \begin{vmatrix} \frac{\partial F}{\partial y}&\frac{\partial F}{\partial z}\\ \frac{\partial G}{\partial y}&\frac{\partial G}{\partial z} \end{vmatrix}.\end{split}\end{aligned}\end{align} \]

Ef við höfum föll $F, G, H$ af breytum $x,y,z,w,\ldots$ þá skilgreinum við, til dæmis,

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\frac{\partial(F,G,H)}{\partial(w,z,y)}= \begin{vmatrix} \frac{\partial F}{\partial w}&\frac{\partial F}{\partial z} &\frac{\partial F}{\partial y}\\ \frac{\partial G}{\partial w}&\frac{\partial G}{\partial z} &\frac{\partial G}{\partial y}\\ \frac{\partial H}{\partial w}&\frac{\partial H}{\partial z} &\frac{\partial H}{\partial y} \end{vmatrix}.\end{split}\end{aligned}\end{align} \]

2.31.4. Setning (Upprifjun á reglu Cramers.)¶

Látum $A$ vera andhverfanlegt $n\times n$ fylki og $\mbox{${\bf b}$}$ vigur í $\mbox{${\bf R}^n$}$. Gerum ráð fyrir að $\mbox{${\bf x}$}=(x_1, x_2, \ldots, x_n)$ sé lausn á $A\mbox{${\bf x}$}=\mbox{${\bf b}$}$. Skilgreinum $B_i$ sem $n\times n$ fylkið sem fæst með því að setja vigurinn $\mbox{${\bf b}$}$ í staðinn fyrir dálk $i$ í $A$. Þá er

\[\displaystyle x_i=\frac{\det B_i}{\det A}.\]

2.31.5. Setning (Setningin um fólgin föllen: implicit function theorem.
Smelltu fyrir ítarlegri þýðingu.)¶

Skoðum jöfnuhneppi

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} F_{(1)}(x_1,\ldots,x_m, y_1, \ldots, y_n)&=0\\ F_{(2)}(x_1,\ldots,x_m, y_1, \ldots, y_n)&=0\\ \vdots\\ F_{(n)}(x_1,\ldots,x_m, y_1, \ldots, y_n)&=0.\end{aligned}\end{split}\end{aligned}\end{align} \]

Látum $P_0=(a_1,\ldots, a_m, b_1,\ldots, b_n)$ vera punkt sem uppfyllir jöfnurnar. Gerum ráð fyrir að allar fyrsta stigs hlutafleiður fallanna $F_{(1)},\ldots, F_{(n)}$ séu samfelldar á opinni kúlu umhverfis $P_0$ og að

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial(F_{(1)}, \ldots, F_{(n)})} {\partial( y_1, \ldots, y_n)}\,\bigg|_{P_0}\neq 0.\end{aligned}\end{align} \]

$\text{Þá eru til föll} \qquad \varphi_1(x_1,\ldots,x_m),\ldots,\varphi_n(x_1,\ldots,x_m)$

á opinni kúlu $B$ umhverfis $(a_1,\ldots,a_m)$ þannig að

\[\displaystyle \varphi_1(a_1,\ldots,a_m)=b_1,\ldots,\varphi_n(a_1,\ldots,a_m)=b_n \qquad \text{og}\]

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} F_{(1)}(x_1,\ldots,x_m, \varphi_1(x_1,\ldots,x_m),\ldots, \varphi_n(x_1,\ldots,x_m))&=0\\ F_{(2)}(x_1,\ldots,x_m, \varphi_1(x_1,\ldots,x_m),\ldots, \varphi_n(x_1,\ldots,x_m))&=0\\ \vdots\\ F_{(n)}(x_1,\ldots,x_m, \varphi_1(x_1,\ldots,x_m),\ldots, \varphi_n(x_1,\ldots,x_m))&=0\end{aligned}\end{split}\end{aligned}\end{align} \]

fyrir alla punkta $(x_1,\ldots,x_m)$ í $B$. Enn fremur fæst að

\[ \begin{align}\begin{aligned}\displaystyle\\\frac{\partial \varphi_i}{\partial x_j} =\frac{\partial y_i}{\partial x_j} =-\frac{\frac{\partial(F_{(1)}, \ldots, F_{(n)})} {\partial( y_1, \ldots,x_j,\ldots y_n)}} {\frac{\partial(F_{(1)}, \ldots, F_{(n)})}{\partial( y_1, \ldots, y_n)}}.\end{aligned}\end{align} \]

2.31.6. Setning (Setningin um staðbundna andhverfu)¶

Látum

\[ \begin{align}\begin{aligned}\displaystyle\\\mbox{${\bf f}$}(x_1,\ldots, x_n)=(f_1(x_1,\ldots,x_n),\ldots,f_n(x_1,\ldots,x_n))\end{aligned}\end{align} \]

vera vörpun af $n$ breytistærðum sem tekur gildi í $\mbox{${\bf R}^n$}$ og er skilgreind á opnu mengi í $\mbox{${\bf R}^n$}$. Gerum ráð fyrir að allar fyrsta stigs hlutafleiður fallanna $f_1, \ldots, f_n$ séu samfelld föll. Ef Jacobi-fylkið $D\mbox{${\bf f}$}(\mbox{${\bf x}$}_0)$ er andhverfanlegt í punkti $\mbox{${\bf x}$}_0$ á skilgreiningarsvæði $\mbox{${\bf f}$}$ þá er til opin kúla $B_{\mbox{${\bf x}$}}$ utan um $\mbox{${\bf x}$}_0$ og opin kúla $B_{\mbox{${\bf y}$}}$ utan um $\mbox{${\bf y}$}_0=f(\mbox{${\bf x}$}_0)$ og vörpun | $\mbox{${\bf g}$}:B_{\mbox{${\bf y}$}}\rightarrow B_{\mbox{${\bf x}$}}$ þannig að $\mbox{${\bf g}$}(\mbox{${\bf f}$}(\mbox{${\bf x}$}))=\mbox{${\bf x}$}$ fyrir alla punkta $\mbox{${\bf x}$}\in B_{\mbox{${\bf x}$}}$ og $\mbox{${\bf f}$}(\mbox{${\bf g}$}(\mbox{${\bf y}$}))=\mbox{${\bf y}$}$ fyrir alla punkta $\mbox{${\bf y}$}\in B_{\mbox{${\bf y}$}}$.

2.31.7. Upprifjun (Taylor-regla í einni breytistærð.)¶

Látum $f$ vera $n+1$-diffranlegt fall af einni breytistærð. Margliðan

\[ \begin{align}\begin{aligned}\displaystyle\\P_{(n)}(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2 +\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n\end{aligned}\end{align} \]

kallast $n$-ta stigs Taylor-margliða $f$ með miðju í $a$. Til er punktur $s$ á milli $a$ og $x$ þannig að

\[\displaystyle E_{(n)}(x)=f(x)-P_{(n)}(x)=\frac{f^{(n+1)}(s)}{(n+1)!}(x-a)^{n+1}.\]

Fáum svo að

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} &f(x)=P_{(n)}(x)+E_{(n)}(x) \\ &=f(a)+f'(a)(x-a)+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n +\frac{f^{(n+1)}(s)}{(n+1)!}(x-a)^{n+1}, \end{aligned}\end{split}\end{aligned}\end{align} \]

sem er kallað $n$-ta stigs Taylor-formúla.

2.31.8. Skilgreining¶

Látum $f(x,y)$ vera fall þannig að fyrsta stigs hlutafleiður $f$ eru skilgreindar og samfelldar. Margliðan

\[\displaystyle P_{(1)}(x,y)=f(a,b)+f_1(a,b)(x-a)+f_2(a,b)(y-b)\]

kallast fyrsta stigs Taylor-margliða $f$ með miðju í $(a,b)$.

2.31.9. Skilgreining¶

Látum $f(x,y)$ vera fall þannig að fyrsta og annars stigs hlutafleiður $f$ eru skilgreindar og samfelldar. Margliðan

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} P_{(2)}&(x,y)=f(a,b)+f_1(a,b)(x-a)+f_2(a,b)(y-b)\\ &+\frac{1}{2}\big(f_{11}(a,b)(x-a)^2+ 2f_{12}(a,b)(x-a)(y-b)+f_{22}(a,b)(y-b)^2\big)\end{aligned}\end{split}\end{aligned}\end{align} \]

kallast annars stigs Taylor-margliða $f$ með miðju í $(a,b)$.

2.31.10. Skilgreining og athugasemd¶

Skilgreinum tvo diffurvirkjaen: differential operator.
Smelltu fyrir ítarlegri þýðingu. $D_1$ og $D_2$ þannig að

\[ \begin{align}\begin{aligned}\displaystyle\\D_1f(a,b)=f_1(a,b)\qquad\mbox{og}\qquad D_2f(a,b)=f_2(a,b).\end{aligned}\end{align} \]

Athugið að ef hlutafleiður $f$ af nógu háum stigum eru allar skilgreindar og samfelldar þá er $D_1D_2=D_2D_1$, þ.e.a.s. ekki skiptir máli í hvaða röð er diffrað, bara hve oft er diffrað með tilliti til hvorrar breytu.

2.31.11. Upprifjun (Tvíliðureglaen: binomial theorem.
Smelltu fyrir ítarlegri þýðingu.)¶

Skilgreinum

\[\displaystyle {n\choose j}=\frac{n!}{j!(n-j)!}.\]

Talan ${n\choose j}$ (lesið $n$ yfir $j$) er $j+1$ talan í $n+1$ línu Pascals-þríhyrningsins. Höfum að

\[\displaystyle (x+y)^n=\sum_{j=0}^n \textstyle{n\choose j}x^jy^{n-j}.\]

2.31.12. Regla¶

Ef $f(x,y)$ er fall þannig að allar hlutafleiður af $n$-ta og lægri stigum eru samfelldar þá gildir að

\[ \begin{align}\begin{aligned}\displaystyle\\(hD_1+kD_2)^nf(a,b)=\sum_{j=0}^n \textstyle{n\choose j} h^jk^{n-j}D_1^jD_2^{n-j}f(a,b).\end{aligned}\end{align} \]

2.31.13. Skilgreining¶

Fyrir fall $f(x,y)$ þannig að allar hlutafleiður af $n$-ta og lægri stigum eru samfelldar þá er $n$-ta stigs Taylor-margliða $f$ með miðju í punktinum $(a,b)$ skilgreind sem margliðan

\[ \begin{align}\begin{aligned}\displaystyle\\\begin{split}\begin{aligned} P_{(n)}(x,y)&= \sum_{m=0}^n \frac{1}{m!}((x-a)D_1+(y-b)D_2)^m f(a,b)\\ &=\sum_{m=0}^n\sum_{j=0}^m \frac{1}{m!}\textstyle{m\choose j} D_1^jD_2^{m-j}f(a,b)(x-a)^j(y-b)^{m-j}\\ &=\sum_{m=0}^n\sum_{j=0}^m \frac{1}{j!(m-j)!} D_1^jD_2^{m-j}f(a,b)(x-a)^j(y-b)^{m-j}.\end{aligned}\end{split}\end{aligned}\end{align} \]

2.31.14. Setning¶

Fyrir fall $f(x,y)$ þannig að allar hlutafleiður af $n+1$-ta og lægri stigum eru samfelldar þá gildir um skekkjuna í $n$-ta stigs Taylor-nálgun að til er tala $\theta$ á milli 0 og 1 þannig að ef $h=x-a$ og $k=y-b$ þá er

\[ \begin{align}\begin{aligned}\displaystyle\\f(x,y)-P_{(n)}(x,y)=\frac{1}{(n+1)!}(hD_1+kD_2)^{n+1} f(a+\theta h, b+\theta k).\end{aligned}\end{align} \]