5. Mismunaaðferðir¶

Við byrjum á að skoða praktískar og tölulegar aðferðir til þess að nálga lausnir á afleiðujöfnum og hlutafleiðujöfnum með upphafs- og jaðarskilyrðum.

Fyrsta aðferðin sem við ætlum að fjalla um er mismunaaðferðen: difference method.
Smelltu fyrir ítarlegri þýðingu.. Það eru ýmsar útgáfur fyrir mismunaaðferðir, en aðalatriði mismunaaðferða er að þær umbreyta afleiðujöfnum (eða hlutafleiðujöfnum) í algebrujöfnuhneppi.

5.1. Mismunaaðferð fyrir venjulegar afleiðujöfnur¶

Við skoðum fyrst jaðargildisverkefni fyrir almenna annars stigs afleiðujöfnu á bili \([a,b]\):

(1)\[\begin{split}\begin{cases} Lu=a_2u''+a_1u'+a_0u=f,& \text{ á } ]a,b[\\ B_1u=\alpha_1u(a)-\beta_1u'(a)=\gamma_1,&(\alpha_1,\beta_1)\neq (0,0),\\ B_2u=\alpha_2u(b)+\beta_2u'(b)=\gamma_2,&(\alpha_2,\beta_2)\neq (0,0). \end{cases}\end{split}\]

Við gerum ráð fyrir að raungildu föllin \(a_0, a_1,a_2\) séu samfelld í \([a,b]\) og fallið \(f\) sé raungilt.

Við veljum skiptingu á bilinu \([a,b]\), þ.e.

\[\begin{split}a=x_0<x_1<x_2<\cdots <x_N=b.\end{split}\]

Til þess að einfalda reikninga getum við valið að skipta bilinu í jafna hluta, þ.e.

\[h:= {b-a\over N}, \qquad x_j=a+jh, \quad j=0, \dots, N.\]

Athugum að þá gildir \(x_{j-1}=x_j-h\) og \(x_{j+1}=x_j+h\).

Við finnum gildi afleiðujöfnunnar í punktunum \(x_j\):

\[\begin{split}\begin{cases} \alpha_1u(x_0)-\beta_1u'(x_0)=\gamma_1,\\ a_2(x_j)u''(x_j)+a_1(x_j)u'(x_j)+a_0(x_j)u(x_j)=f(x_j), \qquad j=1,\dots,N-1,\\ \alpha_2u(x_N)+\beta_2u'(x_N)=\gamma_2. \end{cases}\end{split}\]

Við þurfum að finna nálgun fyrir afleiður \(u'(x_j),u''(x_j)\). Það er eðlilegt að nálga afleiður \(u'(x_j),u''(x_j)\) með samsvarandi mismunakvóta.

Við ætlum að nota eftirfarandi nálgun

Í vinstri endapunkti \(x_0=a\), notum við

\[u'(x)\approx \dfrac{u(x+h)-u(x)}h\]

Í innri punktum bilsins \(x_1, \dots, x_{N-1}\), notum við

(2)\[u'(x)\approx \dfrac{u(x+h)-u(x-h)}{2h} \qquad \text{ og } \qquad u''(x)\approx \dfrac{u(x-h)-2u(x)+u(x+h)}{h^2},\]

Í hægri endapunkti \(x_N=b\), notum við

\[u'(x)\approx \dfrac{u(x)-u(x-h)}h,\]

Hugmyndin er að umrita hneppi (1) með nálgununum að ofan og finna lausnir \(u(x_j)\).

Af hverjum veljum við nálgunarformúlur (1)? Við metum skekkju í nálgunarformúlunum sem við höfum skrifað að ofan. Gerum ráð fyrir að fall \(\varphi\in C^4(I)\) á bili \(I\), og \(x, x+h, x-h\) séu í \(I\). Þá er

\[\begin{split}\begin{aligned} \varphi(x+h)&=\varphi(x)+\varphi'(x)h+\tfrac 12 \varphi''(x)h^2 +\tfrac 16 \varphi'''(x)h^3+\tfrac 1{24}\varphi^{(4)}(\xi)h^4,\\ \varphi(x-h)&=\varphi(x)-\varphi'(x)h+\tfrac 12 \varphi''(x)h^2 -\tfrac 16 \varphi'''(x)h^3+\tfrac 1{24}\varphi^{(4)}(\eta) h^4,\end{aligned}\end{split}\]

þar sem \(\xi \in (x,x+h)\) og \(\eta \in (x-h,x)\).

Við berum saman mismunandi nálgunarformúlur fyrir fyrsta stigs afleiður:

\[\begin{split}\begin{aligned} \varphi'(x)&-\dfrac{\varphi(x+h)-\varphi(x)}h =-\tfrac 12 \varphi''(x)h -\tfrac 16 \varphi'''(x)h^2-\tfrac 1{24}\varphi^{(4)}(\xi)h^3,\\ \varphi'(x)&-\dfrac{\varphi(x)-\varphi(x-h)}h =\tfrac 12 \varphi''(x)h -\tfrac 16 \varphi'''(x)h^2+\tfrac 1{24}\varphi^{(4)}(\eta)h^3,\\ \varphi'(x)&-\dfrac{\varphi(x+h)-\varphi(x-h)}{2h} =-\tfrac 1{12}\varphi'''(x)h^2-\tfrac 1{48} \big(\varphi^{(4)}(\xi)-\varphi^{(4)}(\eta)\big) h^3. \end{aligned}\end{split}\]

Fyrir annars stigs afleiður höfum við:

\[\varphi''(x)-\dfrac{\varphi(x-h)-2\varphi(x)+\varphi(x+h)}{h^2} =-\tfrac 1{24} \big(\varphi^{(4)}(\xi)+\varphi^{(4)}(\eta)\big) h^2.\]

Við sjáum að ef við notum nálgunarformúluna (2) þá er skekkjan af öðru stigi í \(h\). Ef við notum fyrstu tvær formúlurnar, þá er skekkjan af fyrsta stigi í \(h\). Það segir okkur að þegar \(h \ll 1\), þá stefnir skekkjan í nálgunarformúlunni sem við viljum nota hraðar á núll, sem er auðvitað miklu betra.

Til þess að einfalda rithátt skrifum við \(u_j=u(x_j)\) og \(f_j=f(x_j)\). Ennfremur, til þess að leggja áherslu á að \(u_j=u(x_j)\) er óþekkt stærð sem við viljum reikna út, setjum við að lokum \(c_j\) í staðinn fyrir \(u_j=u(x_j)\).

Mismunajafna í vinstri endapunkti

Í vinstri endapunkti \(x_0=a\) höfum við

\[\alpha_1u(x_0)-\beta_1u'(x_0)=\gamma_1.\]

Við nálgum afleiðuna eins og að ofan, þá fáum við

\[\alpha_1 u_0-\beta_1\dfrac{u_1-u_0}h\approx \gamma_1,\]

og að lokum notum við \(c_j\)

\[\alpha_1c_0-\beta_1\dfrac{c_1-c_0}h= \gamma_1.\]

Mismunajafna í innri punktum bilsins

Í innri punktum bilsins \(x_1, \dots, x_{N-1}\), notum við nálgunarformúlur (2), og að lokum fáum við

\[a_2(x_j)\dfrac{u_{j-1}-2u_j+u_{j+1}}{h^2}+a_1(x_j) \dfrac{u_{j+1}-u_{j-1}}{2h}+a_0(x_j)u_j\approx f_j,\]

og fyrir \(c_j\)

\[a_2(x_j)\dfrac{c_{j-1}-2c_j+c_{j+1}}{h^2}+a_1(x_j) \dfrac{c_{j+1}-c_{j-1}}{2h}+a_0(x_j)c_j=f_j.\]

Mismunajafna í hægri endapunkti

Í hægri endapunkti \(x_N=b\), notum við nálgarformúluna að ofan, þá fæst

\[\alpha_2u_N+\beta_2\dfrac{u_N-u_{N-1}}h\approx \gamma_2,\]

og fyrir \(c_{N-1}\) og \(c_N\) þá er

\[\alpha_2c_N+\beta_2\dfrac{c_N-c_{N-1}}h = \gamma_2.\]

Hneppið

Að lokum tökum við saman nálgunarjöfnurnar í \((N+1)\times(N+1)\) hneppi:

\[\begin{split}\begin{cases} \alpha_1c_0-\beta_1\dfrac{c_1-c_0}h= \gamma_1,\\ a_2(x_j)\dfrac{c_{j-1}-2c_j+c_{j+1}}{h^2}+a_1(x_j) \dfrac{c_{j+1}-c_{j-1}}{2h}+a_0(x_j)c_j=f_j,\\ \alpha_2c_N+\beta_2\dfrac{c_N-c_{N-1}}h = \gamma_2, \end{cases}\end{split}\]

sem við getum umskrifað sem

(3)\[\begin{split}\begin{cases} \big(\alpha_1+\tfrac {\beta_1}h\big)c_0 -\tfrac {\beta_1}h c_1= \gamma_1,\\ \big(\tfrac{a_2(x_j)}{h^2}-\tfrac{a_1(x_j)}{2h}\big) c_{j-1} +\big(-\tfrac{2a_2(x_j)}{h^2}+a_0(x_j)\big)c_j +\big(\tfrac{a_2(x_j)}{h^2}+\tfrac{a_1(x_j)}{2h}\big) c_{j+1} =f_j, \qquad j=1, \dots, N-1,\\ -\tfrac{\beta_2}h c_{N-1}+\big(\alpha_2+\tfrac{\beta_2}h \big) c_N = \gamma_2. \end{cases}\end{split}\]

5.1.1. Sýnidæmi¶

Við lítum á eftirfarandi jaðargildisverkefni:

\[\begin{split}\begin{cases} &\left(x^2+1\right) u''(x)-2 x u'(x)+2 u(x)=1,\qquad x \in ]0,1[\\ &u'(0)+u(0)=0,\\ &u(1)=1. \end{cases}\end{split}\]

Fyrst skiptum við bilinu jafnt í tvo hluta, þ.e.

\[x_0=0, \qquad x_1= 1/2 , \qquad x_2 = 1, \qquad N=2, \qquad h={1 \over 2},\]

og við notum nálgunarjöfnurnar (3), og þá fáum við

\[\begin{split}\begin{cases} & 2 c_1-c_0=0, \\ & c_2-1=0,\\ & 6 c_0-8 c_1+4 c_2=1 \end{cases}\end{split}\]

sem gefur okkur

\[c_0= -{3\over 2}, \qquad c_1 = -{3\over 4}, \qquad c_2 =1.\]

Ef við veljum \(N=4\), þ.e.

\[x_0=0, \quad x_1= 1/4 , \quad x_2 = 1/2, \quad x_3 = 3/4, \quad x_4 = 1, \qquad N=4, ~~h={1 \over 4},\]

þá fáum við

\[\begin{split}\begin{cases} & 3 c_0 -4 c_1=0, \\ & c_4 =1,\\ & -18 c_0+32 c_1-16 c_2=-1, \\ & 22 c_1 -38 c_2+18 c_3=1, \\ & 28 c_2-48 c_3+22 c_4 =1. \end{cases}\end{split}\]

Lausnin er

\[c_0=-{5\over 6},~~ c_1=-{5\over 8}, ~~ c_2 = -{1 \over 4},~~ c_3 = {7\over 24}, ~~ c_4 = 1.\]

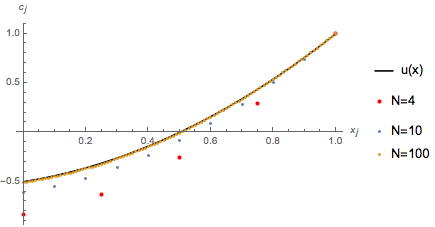
Lausnir fyrir \(N=4, 10, 100\) og lausn \(u(x)={1 \over 2} (2 x^2+x-1).\)

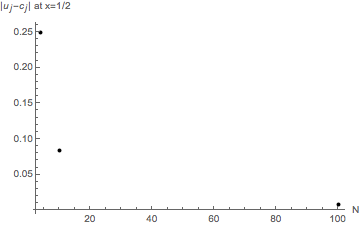
Skekkjan \(|u_j-c_j|\) í \(x=1/2\) sem fall af \(N\).

5.2. Heildun yfir hlutbil¶

Við skoðum nú tilfelli þegar afleiðuvirkinn er af Sturm-Liouville gerð, þ.e.

\[L u= -(p u^\prime)^\prime+ q u,\]

þar sem við gerum ráð fyrir að fallið \(p\) sé samfellt diffranlegt á bili \([a,b]\), og fallið \(p\) sé samfellt á \([a,b]\).

Jaðargildisverkefnið er af gerðinni

\[\begin{split}\begin{cases} Lu=-(pu')'+qu=f,& \text{á } ]a,b[\\ \alpha_1u(a)-\beta_1u'(a)=\gamma_1,\\ \alpha_2u(b)+\beta_2u'(b)=\gamma_2. \end{cases}\end{split}\]

Látum \([c,d]\) vera hlutbil af bilinu \([a,b]\). Við heildum jöfnuna yfir \(x\in [c, d]\), þá er

\[p(c)u'(c)-p(d)u'(d) +\int_c^d q(x)u(x)\, dx=\int_c^d f(x)\, dx.\]

Við viljum finna nálgunarjöfnur fyrir jöfnuna að ofan. Við notum mismunakvóta til þess að nálga afleiður. Við veljum skiptingu

\[\begin{split}x_0 < x_1 < \dots < x_N.\end{split}\]

Við nálgum heildi með Riemann-summu með miðpunktsnálgun:

\[\int_{x_0}^{x_N} \varphi(x)dx= \sum\limits_{j=0}^{N-1} \varphi(m_j)h,\]

þar sem \(m_j\) eru miðpunktar hlutbilanna

\[\begin{split}& m_j= {x_j+ x_{j+1}\over 2}, \qquad j=0, \dots, N-1,\\ & h = {x_N - x_{0}\over N},\\ & x_j= x_0+ j h, \qquad j=0, \dots, N.\end{split}\]

Athugum að

\[m_j= {x_j+ x_{j+1}\over 2}= x_j+ {1\over 2} h, \qquad j=0, \dots, N-1.\]

Eins og við gerðum í 5.1, þurfum við að skoða jaðarskilyrðin hvert í sínu lagi.

Til þess að einfalda rithátt, fyrir öll \(j\) táknum við

\[\begin{split}& u_j=u(x_j), ~~~ f_j=f(x_j), ~~~ p_j=p(x_j),~~~ q_j=q(x_j), \\ & p_{j+\frac 12}=p(m_j).\end{split}\]

Mismunajafna í vinstri endapunkti bilsins

Við heildum yfir hlutbilið \([x_0, m_0]\). Athugum að \(m_0-x_0=\frac 12 h\). Við fáum

\[p(x_0)u'(x_0)-p(m_0)u'(m_0) +\int_{x_0}^{m_0} qu\, dx=\int_{x_0}^{m_0} f\, dx,\]

sem gefur okkur

\[u'(x_0)=\dfrac 1{p(x_0)}\bigg(p(m_0)u'(m_0) -\int_{x_0}^{m_0}q(x)u(x)\, dx +\int_{x_0}^{m_0}f(x)\, dx\bigg).\]

Við nálgum heildið með

\[\begin{split}&\int_{x_0}^{m_0}q(x)u(x) dx\approx \frac 12 h q(x_0) u(x_0) = \frac 12 h q_0 u_0, \\ & \int_{x_0}^{m_0}f(x) dx\approx \frac 12 h f(x_0)= \frac 12 h f_0.\end{split}\]

Við nálgum afleiðuna \(u'(m_0)\) með mismunakvóta:

\[u'(m_0)\approx {u(x_1)-u(x_0)\over 2 h/2}= {u_1-u_0\over h}.\]

Þá er \(u'(x_0)\)

\[u'(x_0)\approx\dfrac 1{p_0}\bigg(p_{\frac 12} {u_1-u_0\over h} -\frac 12 h q_0 u_0 +\frac 12 h f_0\bigg).\]

Nú notum við jaðarskilyrði í \(x_0\):

\[\alpha_1u(a)-\beta_1u'(a)=\gamma_1\]

sem er nú

\[\alpha_1u_0-\dfrac {\beta_1}{p_0}\bigg( p_{\frac 12}\dfrac{u_1-u_0}{h} -\tfrac 12 h q_0u_0+ \tfrac 12 hf_0\bigg)\approx \gamma_1.\]

Eins og áður setjum við \(c_0, c_1\) í staðinn fyrir \(u_0, u_1\) til þess að tákna óþekkta stærð:

\[\alpha_1 c_0-\dfrac {\beta_1}{p_0}\bigg( p_{\frac 12}\dfrac{c_1-c_0}{h} -\tfrac 12 h q_0c_0+\tfrac 12 hf_0\bigg)=\gamma_1.\]

Mismunajafna í hægri endapunkti

Við gerum svipað fyrir hlutbilið \([ m_{N-1}, x_N]\):

\[u'(x_N)=\dfrac 1{p(x_N)}\bigg(p(m_{N-1})u'(m_{N-1}) +\int_{m_{N-1}}^{x_N}q(x)u(x)\, dx- \int_{m_{N-1}}^{x_N}f(x)\, dx\bigg).\]

Við nálgum heildið með

\[\begin{split}& \int_{m_{N-1}}^{x_N}q(x)u(x)\, dx \approx \tfrac 12h q_Nu_N, \\ & \int_{m_{N-1}}^{x_N}f(x)\, dx \approx \tfrac 12h f_N,\end{split}\]

og afleiðuna \(u'(x_{N-1})\) með formúlunni

\[u'(m_{N-1}) \approx\dfrac{u_N-u_{N-1}}{h}.\]

Þá getum við nálgað jaðarskilyrðið í \(x_N\)

\[\alpha_2u(x_N)+\beta_2u'(x_N)=\gamma_2\]

með

\[\alpha_2u_N+\dfrac {\beta_2}{p_N}\bigg( p_{N-\frac 12}\dfrac{u_N-u_{N-1}}{h}+\tfrac 12h q_Nu_N -\tfrac 12h f_N\bigg)\approx\gamma_2.\]

Mismunajöfnur í innri punktum skiptingarinnar

Nú skoðum við hlutbilin \([m_{j−1}, m_j ]\) fyrir \(j=1, \dots, N-1\). Athugum að \(x_j\) eru miðpunktar bilanna \([m_{j−1}, m_j ]\).

Við heildum jöfnuna yfir \([m_{j−1}, m_j ]\)

\[p(m_{j-1})u'(m_{j-1})-p(m_j)u'(m_j)+\int_{m_{j-1}}^{m_j}q(x)u(x)\, dx =\int_{m_{j-1}}^{m_j}f(x)\, dx.\]

Við nálgum heildið með miðpunktsnálgun

\[\int_{m_{j-1}}^{m_j}q(x)u(x)\, dx \approx h\ q_ju_j \qquad \text{ og } \qquad \int_{m_{j-1}}^{m_j}f(x)\, dx \approx h\ f_j,\]

og afleiður með mismunakvótum

\[u'(m_j)\approx \dfrac{u_{j+1}-u_j}h \qquad \text{ og } \qquad u'(m_{j-1})\approx \dfrac{u_j-u_{j-1}}h.\]

Þá verður jafnan

\[p_{j-\frac 12}\dfrac{u_j-u_{j-1}}h -p_{j+\frac 12}\dfrac{u_{j+1}-u_j}h +h q_ju_j\approx hf_j,\]

og þegar við stingum \(c_j\) í jöfnuna í staðinn fyrir \(u_j\), fáum við

\[p_{j-\frac 12}\dfrac{c_{j}-c_{j-1}}{h^2} -p_{j+\frac 12}\dfrac{c_{j+1}-c_j}{h^2} +q_jc_j= f_j.\]

Nálgunarjöfnuhneppið

Að lokum, er línulega jöfnuhneppið fyrir nálgunargildin

\[\begin{split}\begin{cases} \bigg(\alpha_1+\dfrac{\beta_1}{p_0} \bigg(\dfrac{p_{\frac 12}}h+\tfrac 12 hq_0\bigg)\bigg)c_0 -\dfrac{\beta_1p_{\frac 12}}{p_0h}c_1 =\gamma_1+\tfrac 12 \dfrac{\beta_1hf_0}{p_0}, \\ -\dfrac{p_{j-\frac 12}}{h^2} c_{j-1} +\bigg(\dfrac{p_{j-\frac 12}+p_{j+\frac 12}}{h^2}+q_j\bigg) c_j -\dfrac{p_{j+\frac 12}}{h^2} c_{j+1} =f_j, \qquad j=1, \dots, N-1, \\ -\dfrac{\beta_2p_{N-\frac 12}}{p_Nh}c_{N-1}+ \bigg(\alpha_2+\dfrac{\beta_2}{p_N}\bigg(\dfrac{p_{N-\frac 12}}{h}+\tfrac 12 h q_N\bigg)\bigg)c_N =\gamma_2+\tfrac 12\dfrac{\beta_2h}{p_N}f_N. \end{cases}\end{split}\]

5.2.1. Sýnidæmi¶

Við endurtökum nú sýnidæmi 5.1.1. Við sjáum að

\[\begin{split}& p(x)=\frac{1}{x^2+1}, \quad q(x)=-\frac{2}{\left(x^2+1\right)^2},\quad \rho=-\frac{1}{\left(x^2+1\right)^2}, \\ & \mathcal L u = {1\over \rho} \left( -(p u^\prime)^\prime +q u\right) = \widetilde{f}, \\ & \Rightarrow \left( -(p u^\prime)^\prime +q u\right) = \rho \widetilde{f} := f,\end{split}\]

þar sem \(f(x)= -\frac{1}{\left(x^2+1\right)^2}\). Þá er jaðargildisverkefnið af gerðinni

\[\begin{split}\begin{cases} u''(x)-\frac{2 x u'(x)}{x^2+1}+\frac{2 u(x)}{x^2+1}=\frac{1}{x^2+1},\\ u'(0)+u(0)=0,\\ u(1)=1. \end{cases}\end{split}\]

Við notum nálgunarformúlurnar að ofan fyrir \(N=4\). Athugum að

\[\begin{split}& x_0= 0, ~~ x_1= \frac{1}{4}, ~~ x_2=\frac{1}{2}, ~~ x_3=\frac{3}{4}, ~~ x_4=1,\\ & m_0=\frac{1}{8}, ~~ m_1=\frac{3}{8}, ~~ m_2=\frac{5}{8}, ~~ m_3=\frac{7}{8}.\end{split}\]

Línulega hneppið er

\[\begin{split}\begin{cases} 1398 c_0-2048 c_1=-65, \\ c_4=1, \\ 84388 c_0-150038 c_1+75140 c_2=4745,\\ 142400 c_1-246206 c_2+116800 c_3=6497, \\ 282500 c_2-484886 c_3+222500 c_4 =10057, \end{cases}\end{split}\]

sem gefur okkur

\[c_0= -0.4895, c_1=-0.3024, c_2= 0.0091, c_3= 0.4434, c_4= 1.\]

Er þetta betra en í dæmi 5.1.1? Skoðum myndina.

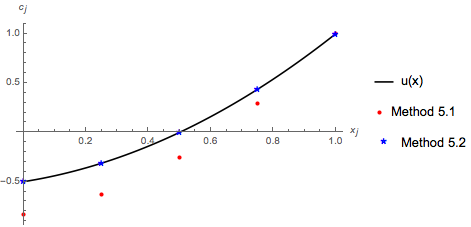
5.2.2. Línuleg brúun og þúfugrunnföll¶

Við höfum reiknað út lausnir \(c_j\) á nálgunarformúlunni. Hvernig getum við endurgert fallið \(u\) sem uppfyllir \(u_j \approx c_j\)? Við getum notað línulega samantekt til að finna nálgunarfall \(v\in C[a,b]\), þ.a. \(v(x_j)= c_j\) og svo \(v_j \approx u_j\).

Fyrst skilgreinum við þúfugrunnföllin \(\varphi_j(x)\), fyrir \(j=0, \dots, N\), þ.a.

\(\varphi_j(x)\) eru samfelld,
\(\varphi_j(x_i)=\delta_{i,j}\).

Við tökum t.d. jafna skiptingu á bilinu \([a,b]\)

\[\begin{split}a=x_0<x_1<x_2<\cdots <x_N=b, \qquad x_j= a + j h, \qquad j=0, \dots, N,\end{split}\]

þá eru föllin \(\varphi_j(x)\) af gerðinni

\[\begin{split}\begin{aligned} \varphi_0(x)&=\begin{cases} \tfrac{x_1-x}{h}, &x\in [x_0,x_1],\\ 0, &\text{annars}, \end{cases} & \varphi'_0(x)&=\begin{cases} \tfrac{-1}{h}, &x\in ]x_0,x_1[,\\ 0, &x\in {{\mathbb R}}\setminus [x_0,x_1], \end{cases} \nonumber \\ \varphi_j(x)&=\begin{cases} \tfrac{x-x_{j-1}}{h}, &x\in [x_{j-1},x_j[,\\ \tfrac{x_{j+1}-x}{h}, &x\in [x_j,x_{j+1}],\\ 0, &\text{annars}. \end{cases}& \varphi'_j(x)&=\begin{cases} \tfrac{1}{h}, &x\in ]x_{j-1},x_j[,\\ \tfrac{-1}{h}, &x\in [x_j,x_{j+1}],\\ 0, &x\in {{\mathbb R}}\setminus [x_{j-1},x_{j+1}]. \end{cases} \\ \varphi_N(x)&=\begin{cases} \tfrac{x-x_{N-1}}{h}, &x\in [x_{N-1},x_N],\\ 0, &\text{annars}. \nonumber \end{cases}& \varphi'_N(x)&=\begin{cases} \tfrac{1}{h}, &x\in [x_{m-1},x_m],\\ 0, &\text{annars}. \nonumber \end{cases}\end{aligned}\end{split}\]

Athugum að föllin \(\varphi_j(x)\) eru samfelld á \([a,b]\).

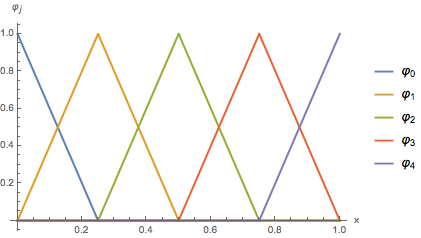
Þúfugrunnföllin \(\varphi_j(x)\) fyrir dæmin 5.1.1 og 5.2.1. Hér \(N=4\).

Þá skilgreinum við nálgunarfall \(v\), með því að setja

\[v(x)=c_0\varphi_0(x)+\cdots+c_N\varphi_N (x),\]

þar sem \(c_j\) eru lausnir á nálgunarformúlunni. Það er ljóst að \(v\) er samfellt á bilinu \([a,b]\), og

\[v(x_j)= \sum_{i=0}^N c_i\varphi_i(x_j)= c_j.\]

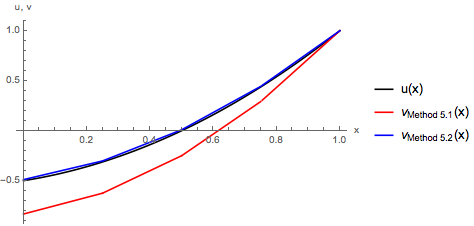
Nálgunarföllin \(v\) fyrir dæmin 5.1.1 og 5.2.1. Hér \(N=4\).

5.3. Mismunaaðferð fyrir hlutaafleiðujöfnur¶

Nú lítum við á verkefnið að nálga lausnir á hlutafleiðujöfnum með upphafs- og jaðarskilyrðum.

Látum \(D\) vera svæði í \(R^2\) og skoðum eftirfarandi jaðargildisverkefni

\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu= -p\nabla^2u-\nabla p\cdot \nabla u+qu=f, \qquad \text{ á } D\\ \alpha u+\beta\dfrac{\partial u}{\partial n} =\gamma, \qquad \text{á } \ \partial D. \end{cases}\end{split}\]

Við gerum ráð fyrir að \(p\in C^1(\mathbb R^2)\) og \(q, f\) séu samfelld á \(\mathbb R^2\). \(\alpha,\beta\) og \(\gamma\) séu gefin föll á jaðrinum \(\partial D\) þ.a. \((\alpha, \beta)\neq (0,0)\) á \(\partial D\).

Látum \(\partial D_1\) vera þann hluta jaðarsins þ.a. \(\beta=0\), þá er \(u(x,y)=\gamma(x,y)/\alpha(x,y)\) fyrir öll \((x,y)\in \partial D_1\). Þá skiptum við jaðrinum í tvö sundurlæg mengi \(\partial D=\partial D_1\cup \partial D_2\), og við umskrifum jaðargildisverkenið sem

(4)\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu=f, \quad &\text{á } D\\ u=\gamma,\quad &\text{á } \ \partial_1 D,\\ \alpha u+\beta\dfrac{\partial u}{\partial n} =\gamma, \quad &\text{á } \ \partial_2 D, \end{cases}\end{split}\]

þar sem höfum við táknað \(\gamma(x,y)/\alpha(x,y)\) með \(\gamma\) á \(\partial_1 D\) að ofan.

Til þess að nálga lausn \(u\) á jaðargildisverkefninu (4) þurfum við að undirbúa net á svipaðan hátt og við gerðum í 5.1. Það sem er ólíkt hér er að við erum í \(\mathbb R^2\), þ.e.a.s. við þurfum að byggja skiptingu eftir \(x\) og \(y\).

Net

Gerum ráð fyrir að svæðið \(D\) sé innihaldið í rétthyrningi

\[R=\{(x,y)\,;\, a\leq x\leq b, c\leq y\leq d\}.\]

Við tökum \(h>0\) og við skiptum bilunum á eftirfarandi hátt

\[x_m=a+mh \qquad \text{ og } \qquad y_n=c+nh, \qquad m,n\in {{\mathbb N}\cup {0}}.\]

Dæmi af \(D \subset R \subset {\mathbb R^2}\).

Hnútpunktar í netinu eru \((x_i, y_k)\) og línurnar gegnum hnútpunktana eru stikaðar með

\[{{\mathbb R}}\ni t\mapsto (a+mh,t) \qquad \text{ og } \qquad {{\mathbb R}}\ni s\mapsto (s,c+nh).\]

Við sjáum að línurnar skera \(\overline D =D\cup\partial D\) í punktinum \((x_i, y_k)\) , \(i=1,\dots, M_1\) og \(k=1,\dots,M_2\).

Við þurfum að velja hvernig við viljum raða punktunum sem eru í \(\overline D\). Til þess að einfalda nálgunarformúlur, er gott að raða punktunum á eftirfarandi hátt:

Setjum \(M = M_1 \times M_2\), og

Allir hnútpunktar eru \((x_j, y_j)\) þar sem \(j=1, \dots, M\),
Hnútpunktar \((x_j, y_j)\) fyrir \(j=1,+dots, N\leq M\) eru í \(D\cup \partial D_2\),
Hnútpunktar \((x_j, y_j)\) fyrir \(j=N+1, \dots, M\) eru í \(\partial D_1\).

Hugmyndin að baki þessu er að fallgildi \(u\) eru þekkt á \(\partial D_1\) af því að \(u\) uppfyllir Dirichlet-jaðarskilyrði þar.

Heildun yfir hlutsvæði

Gerum ráð fyrir að hlutsvæði \(\Omega\) sé í \(D\), t.d. getur \(\Omega\) verið hlutrétthyrningur milli \((x_j,y_j)\) fyrir \(j=1, \dots 4\).

Við heildum jöfnuna yfir \(\Omega\) og við notum Gauss-setninguna sem gefur okkur

\[\iint_\Omega \nabla\cdot\big(p\nabla u\big) \, dxdy =\int_{\partial\Omega} p\dfrac{\partial u}{\partial n}\, ds,\]

þá er jafnan í (4)

\[-\int_{\partial\Omega } p\dfrac{\partial u}{\partial n}\, ds +\iint_\Omega qu\, dxdy =\iint_\Omega f\, dxdy.\]

Við ætlum að nota þessi heildi til þess að nálga lausn \(u\) í punktunum \((x_j, y_j)\) fyrir \(j=1,\dots, N\).

5.3.1. Nálgunarjafna¶

Nú erum við tilbúin til að leiða út nálgunarjöfnur fyrir jaðargildisverkenið (4). Eins og áður greinum við á milli innri punkta og jaðarpunkta.

Nálgunarjafna í innri punkti

Látum \((x_j, y_j)\) vera innri punkt í \(D\), og \(\Omega_j\) vera ferninginn með miðju í \((x_j, y_j)\) og kantlengdina \(h\). Látum grannpunkta \((x_j, y_j)\) vera \((x_l,y_l), (x_r,y_r), (x_s,y_s)\) og \((x_t,y_t)\). Við táknum með \(m_{j,k}\) miðpunkt línunnar milli \((x_j,y_j)\) og \((x_k,y_k)\), og með \(S_{j,k}\) hlið af \(\partial\Omega_j\) sem er milli \((x_j,y_j)\) og \((x_k,y_k)\). Athugum að hér eru \(j, l, r\), og \(s\) gefin, á meðan lagt er saman yfir \(k=l,r,s, t\).

Við sjáum á myndinni hér:

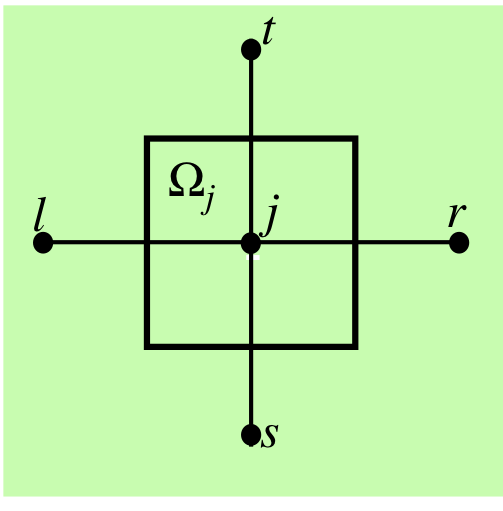
Dæmi af innri punktum \((x_j,y_j)\).

Þá er yfir \(\Omega_j\)

\[\iint_{\Omega_j} \nabla\cdot\big(p\nabla u\big) \, dxdy =\int_{\partial{\Omega}_j} p\dfrac{\partial u}{\partial n}\, ds = \sum_{k=l,r,s,t} \int_{S_{j,k}} p\dfrac{\partial u}{\partial n}\, ds.\]

Við nálgun heildið yfir \(S_{j,k}\) með því að finna gildi fallsins \(p\) og afleiðunnar \({\partial u\over \partial n}\) í miðpunktum \(m_{j,k}\), þá er

\[\int_{S_{j,k}}p\dfrac{\partial u}{\partial n} \, ds \approx p(m_{j,k})\dfrac{\partial u}{\partial n}(m_{j,k}) h \approx p(m_{j,k})\dfrac{u(x_k,y_k)-u(x_j,y_j)}{h} h.\]

Liðirnir sem eftir standa eru nálgaðir með

\[\iint_{\Omega_j}q u \, dxdy \approx q(x_j,y_j)u(x_j,y_j)\, h^2,\]

\[\iint_{\Omega_j}f \, dxdy \approx f(x_j,y_j)\, h^2.\]

Til þess að einfalda rithátt, setjum við \(u_k=u(x_k,y_k), q_k=q(x_k,y_k), f_k=f(x_k,y_k)\) og \(p_{j,k}=p(m_{j,k})\), og að lokum fáum við að jafnan (4) er nálguð með

\[\begin{split}&&-\int_{\partial\Omega } p\dfrac{\partial u}{\partial n}\, ds +\iint_\Omega qu\, dxdy =\iint_\Omega f\, dxdy\\ && \Rightarrow ~~ -p_{j,l}(u_l-u_j) -p_{j,r}(u_r-u_j) -p_{j,s}(u_s-u_j) -p_{j,t}(u_t-u_j) +q_ju_jh^2\approx f_jh^2.\end{split}\]

Við notum \(c_k\) í staðinn fyrir \(u_k\) fyrir \(k=j,l,r,s,t\), og þá er nálgunarformúlan fyrir innri punktana

(5)\[\begin{split}\begin{gathered} \big(h^{-2}\big({p_{j,l}+p_{j,r}+p_{j,s}+p_{j,t}}\big)+q_j\big)c_j \\ -h^{-2}p_{j,l}c_l -h^{-2}p_{j,r}c_r -h^{-2}p_{j,s}c_s -h^{-2}p_{j,t}c_t =f_j. \end{gathered}\end{split}\]

Í sértilfellinu þegar \(p=1\), þá fáum við

(6)\[\big(4{h^{-2}}+q_j\big)c_j -{h^{-2}}c_l -{h^{-2}}c_r -{h^{-2}}c_s -{h^{-2}}c_t =f_j.\]

Nálgunarjafna í jaðarpunkti

Látum \((x_j,y_j)\) vera jaðarpunkt í \(\partial D_2\). Látum grannpunkta \((x_j, y_j)\) vera \((x_l,y_l), (x_s,y_s)\) og \((x_t,y_t)\). Við gerum ráð fyrir að línan \(S_j\) milli miðpunktanna \(m_{j,s}\) og \(m_{j,t}\) sé í \(\partial D_2\). Athugum að hér er \(k=s, l, t\), og hér er flatarmál svæðisins \(\Omega_j\) \(h^2/2\).

Við sjáum á myndinni hér:

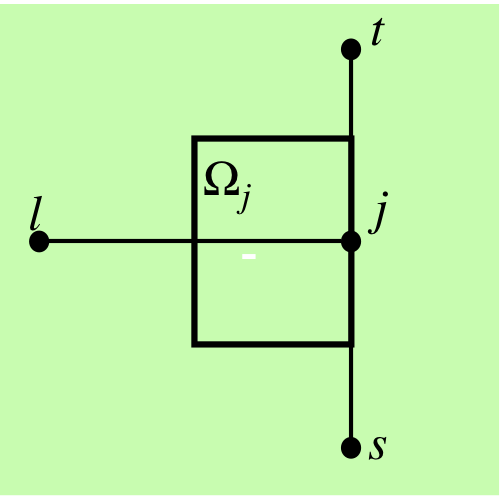
Dæmi af jaðarpunktum \((x_j,y_j)\).

Við höfum

\[\iint_{\Omega_j} \nabla\cdot\big(p\nabla u\big) \, dxdy= \int_{\partial \Omega_j} p\dfrac{\partial u}{\partial n}\, ds =\sum_{k=l,s,t} \int_{S_{j,k}} p\dfrac{\partial u}{\partial n}\, ds +\int_{S_{j}} p\dfrac{\partial u}{\partial n}\, ds.\]

Heildið yfir \(S_j\) er

\[\int_{S_{j}} p\dfrac{\partial u}{\partial n}\, ds \approx p_j \dfrac{\partial u}{\partial n}(x_j,y_j) \approx p_j {\gamma_j-\alpha_j u_j\over \beta_j} h,\]

þar sem við höfum notað jaðarskilyrði á \(\partial D_2\) fyrir \(\dfrac{\partial u}{\partial n}(x_j,y_j)\), og táknað \(\gamma(x_j,y_j), \alpha(x_j,y_j), \beta(x_j,x_j)\) með \(\gamma_j,\alpha_j, \beta_j\).

Heildið yfir \(S_{j,l}\) er

\[\int_{S_{j,l}} p\dfrac{\partial u}{\partial n} \, ds \approx p_{j,l}\dfrac {u_l-u_j} h h,\]

en heildin yfir \(S_{j,s}\) og \(S_{j,t}\) eru gefin með

\[\int_{S_{j,s}} p\dfrac{\partial u}{\partial n} \, ds \approx p_{j,s}\dfrac{u_s-u_j}h\tfrac 12 h \qquad \text{ og } \qquad \int_{S_{j,t}} p\dfrac{\partial u}{\partial n} \, ds \approx p_{j,t}\dfrac{u_t-u_j}h\tfrac 12 h.\]

Að lokum þurfum við að nálga heildið með föllum \(f\) og \(q\)

\[\iint_{\Omega_j} q u\, dxdy \approx q_ju_j \tfrac 12 h^2 \quad \text{ og } \quad \iint_{\Omega_j} f\, dxdy \approx f_j \tfrac 12 h^2.\]

Að lokum að lokum setjum við saman alla liði og þá er

(7)\[\begin{split}\begin{gathered} \big(2h^{-2}p_{j,l}+h^{-2}p_{j,s}+h^{-2}p_{j,t} +2h^{-1}p_j\tfrac{\alpha_j}{\beta_j}+q_j\big)c_j \\ -2h^{-2}p_{j,l}c_l-h^{-2}p_{j,s}c_s-h^{-2}p_{j,t}c_t =f_j+2h^{-1}p_j\tfrac{\gamma_j}{\beta_j}. \end{gathered}\end{split}\]

þar sem við höfum skrifað \(c_j\) í staðinn fyrir \(u_j\).

Í sértilfellinu þegar \(p=1\), þá fáum við

(8)\[\big(4h^{-2} +q_j+2h^{-1}\tfrac{\alpha_j}{\beta_j}\big)c_j -2h^{-2}c_l-h^{-2}c_s-h^{-2}c_t =f_j+2h^{-1}\tfrac{\gamma_j}{\beta_j}\]

Samantekt

Til þess að nálga lausnagildi á jaðargildisverkefninu (4) getum við leyst eftirfarandi jöfnuhneppi:

Fyrir \((x_j, y_j)\in D\):

\[\begin{split}\begin{gathered} \big(h^{-2}\big({p_{j,l}+p_{j,r}+p_{j,s}+p_{j,t}}\big)+q_j\big)c_j \\ -h^{-2}p_{j,l}c_l -h^{-2}p_{j,r}c_r -h^{-2}p_{j,s}c_s -h^{-2}p_{j,t}c_t =f_j.\end{gathered}\end{split}\]

Fyrir \((x_j, y_j)\in \partial D_2\):

\[\begin{split}\begin{gathered} \big(2h^{-2}p_{j,l}+h^{-2}p_{j,s}+h^{-2}p_{j,t} +2h^{-1}p_j\tfrac{\alpha_j}{\beta_j}+q_j\big)c_j \\ -2h^{-2}p_{j,l}c_l-h^{-2}p_{j,s}c_s-h^{-2}p_{j,t}c_t =f_j+2h^{-1}p_j\tfrac{\gamma_j}{\beta_j}.\end{gathered}\end{split}\]

Fyrir \((x_j, y_j)\in \partial D_1\):

\[c_j= \gamma_j \,.\]

5.3.2. Sýnidæmi: Dirichlet-verkefni á ferningi¶

Látum \(D\) vera \(D=\{(x,y)\,;\, 0<x<1, 0<y<1\}\). Við viljum leysa Dirichlet-verkefnið yfir \(D\):

\[\begin{split}\begin{cases} -\nabla^2u+qu=f,&\text{í } D,\\ u(x,y)=\gamma(x,y),& (x,y)\in \partial D. \end{cases}\end{split}\]

Hér erum við í sértilfellinu þegar \(p=1\), og \(\partial D_2\) er ekki til.

Setjum \(h={1\over 3}\). Við röðum punktum þ.a. punktar \((x_j,y_j)\) fyrir \(j=1, \dots, 4\) eru innri punktar og \((x_j,y_j)\) fyrir \(j=5,\dots, 16\) eru jaðarpunktar. Við sjáum þetta á eftirfarandi mynd

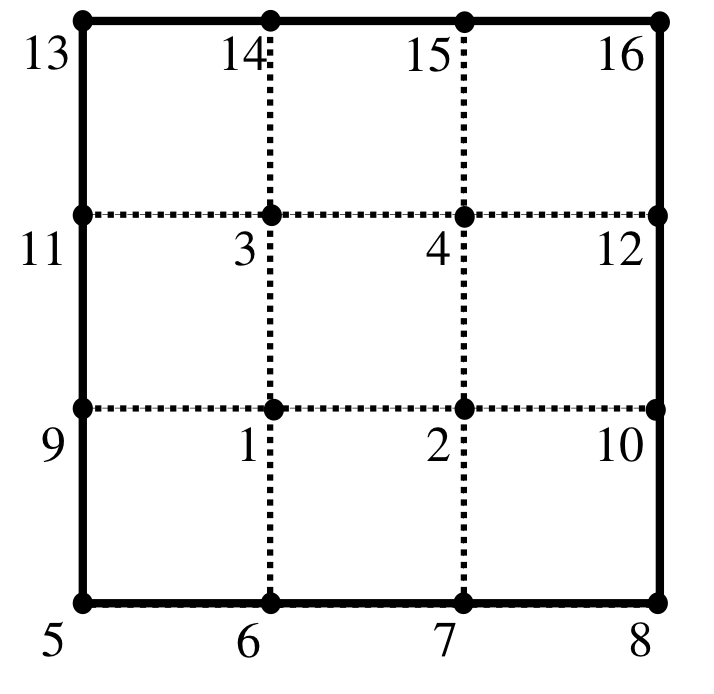
Fyrir punkta \((x_j,y_j)\) með \(j=1, \dots, 4\), notum við nálgunarjöfnur (6), og þá er

\[\begin{split}\begin{aligned} (36+q_1)c_1-9c_2-9c_3-9c_6-9c_9&=f_1,\\ (36+q_2)c_2-9c_1-9c_4-9c_7-9c_{10}&=f_2,\\ (36+q_3)c_3-9c_1-9c_4-9c_{11}-9c_{14}&=f_3,\\ (36+q_4)c_4-9c_2-9c_3-9c_{12}-9c_{15}&=f_4.\\\end{aligned}\end{split}\]

Fyrir punkta \((x_j,y_j)\) með \(j=5,\dots, 16\), notum við nálgunarjöfnur (8), og þá er

\[c_j = \gamma_j.\]

Það þýðir að við getum leyst jöfnuhneppið fyrir \(c_1, \dots, c_4\) og þá höfum við

\[\begin{split}\left[ \begin{matrix} 36+q_1&-9&-9& 0\\ -9&36+q_2&0&-9\\ -9&0&36+q_3&-9\\ 0&-9&-9&36+q_4\\ \end{matrix}\right] \left[ \begin{matrix} c_1\\c_2\\c_3\\c_4 \end{matrix} \right] =\left[ \begin{matrix} f_1+9\gamma_6+9\gamma_9,\\ f_2+9\gamma_7+9\gamma_{10},\\ f_3+9\gamma_{11}+9\gamma_{14},\\ f_4+9\gamma_{12}+9\gamma_{15}.\\ \end{matrix} \right].\end{split}\]

5.3.3. Sýnidæmi: Jaðargildisverkefni á ferningi með blandað jaðarskilyrði¶

Lítum nú á jaðargildisverkefni á \(D=\{(x,y)\,;\, 0<x<1, 0<y<1\}\)

\[\begin{split}\begin{cases} -\nabla^2u+qu=f,&\text{í } D,\\ u(x,y)=\gamma(x,y),& (x,y)\in \partial D_1,\\ \alpha(x,y)u(x,y)+\dfrac{\partial u}{\partial n}(x,y) =\gamma(x,y),& (x,y)\in \partial D_2, \end{cases}\end{split}\]

þar sem

\[\begin{split}\begin{aligned} \partial D_1 &= \{(x,y)\,;\, 0<x<1, 0=y, y=1,~~ \text{og} \quad 0<y<1, x=0 \},\\ \partial D_2 &= \{(x,y)\,;\, 0<y<1, x=1\}. \end{aligned}\end{split}\]

Athugum að hér er \(p=1\) og \(\beta=1\). Setjum \(h={1\over 3}\), og röðum punktum þ.a. \((x_j,y_j)\) fyrir \(j=1,\dots, 6\) eru í \(\partial D_2\) og \((x_j,y_j)\) fyrir \(j=7, \dots, 16\) eru í \(\partial D_1\). Við sjáum þetta á eftirfarandi mynd

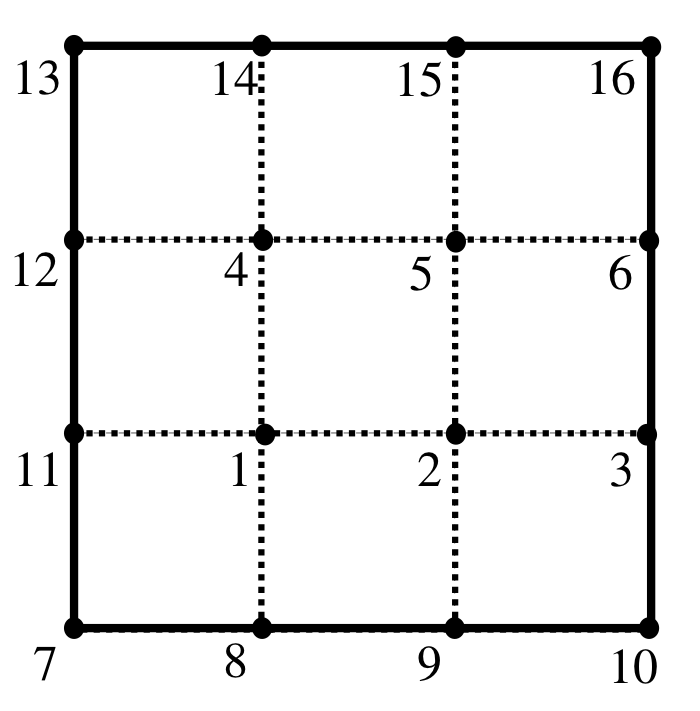
Fyrir punkta \((x_j,y_j)\) með \(j=7,\dots, 16\), þá er

\[c_j = \gamma_j.\]

Fyrir punkta \((x_j,y_j)\) með \(j=1,2,4,5\) notum við nálgunarjöfnur (6), fyrir punkta \((x_j,y_j)\) með \(j=3,6\) notum við nálgunarjöfnur (8), og þá er

\[\begin{split}\begin{aligned} (36+q_1)c_1-9c_2-9c_4-9c_8-9c_{11}&=f_1,\\ (36+q_2)c_2-9c_1-9c_3-9c_5-9c_{9}&=f_2,\\ (36+q_3+6\alpha_3)c_3-18c_2-9c_6-9c_{10}&=f_3+6\gamma_3,\\ (36+q_4)c_4-9c_1-9c_5-9c_{12}-9c_{14}&=f_4.\\ (36+q_5)c_5-9c_2-9c_4-9c_{6}-9c_{15}&=f_5.\\ (36+q_6+6\alpha_6)c_6-9c_3-18c_{5}-9c_{16}&=f_6+6\gamma_6.\\ \end{aligned}\end{split}\]

Við getum skrifað þetta með fylkjajöfnu

\[\begin{split}\begin{gathered} \left[ \begin{matrix} 36+q_1&-9&0&-9& 0& 0\\ -9&36+q_2&-9&0&-9&0\\ 0&-18&36+q_3+6\alpha_3&0&0&-9\\ -9&0&0&36+q_4&-9&0\\ 0&-9&0&-9&36+q_5&-9\\ 0&0&-9&0&-18&36+q_6+6\alpha_6\\ \end{matrix}\right] \left[ \begin{matrix} c_1\\c_2\\c_3\\c_4 \\ c_5 \\ c_6 \end{matrix} \right]\\ =\left[ \begin{matrix} f_1+9\gamma_8+9\gamma_{11}\\ f_2+9\gamma_{9}\\ f_3+9\gamma_{10}+6\gamma_3\\ f_4+9\gamma_{12}+9\gamma_{14}\\ f_5+9\gamma_{15}\\ f_6+9\gamma_{16}+6\gamma_6\\ \end{matrix} \right].\end{gathered}\end{split}\]

5.4. Almenn mismunaaðferð á rétthyrningi¶

Við lítum nú á almennt jaðargildisverkefni

(9)\[\begin{split}\begin{cases} -\nabla\cdot\big(p\nabla u\big)+qu=f, &\text{í } D,\\ \alpha u + \beta \dfrac{\partial u}{\partial n} = \gamma,& \text{á } \partial D, \end{cases}\end{split}\]

á rétthyrningi \(D\) in \(R^2\)

\[\begin{split}D = \ ]a,b[\times ]c,d[ \ = \{(x,y)\, ;\, a<x<b, c<y<d\}.\end{split}\]

Við gerum ráð fyrir að \((\alpha,\beta ) \neq (0,0)\) fyrir \((x,y) \in \partial D\).

Athugum að í hornunum geta föllin \(\alpha, \beta\) og \(\gamma\) verið ósamfelld og afleiðan \(\dfrac{\partial u}{\partial n}\) getur einnig verið ekki vel skilgreind.

Nú skiptum við rétthyrningnum \(D\) í reglulegt net með kantlengdina \(h\). Setjum \(N=(b-a)/h\) og \(M=(d-c)/h\), þ.a. \(N\) og \(M\) eru náttúrlegar tölur.

Hvernig getum við tölusett netpunkta í \(D\)?

Hnit netpunkta í \((x,y)\) plani

Það þýðir að við veljum skiptingu á bilinu í jafna hluta, þ.e.

\[\begin{split}a=x_1<x_2<x_3<⋯<x_{(N+1)}=b, \qquad c=y_1<y_2<y_3<⋯<y_{(M+1)}=d,\end{split}\]

og

\[x_j=a+(j-1) h, \quad j=1, \dots, N+1\,,\qquad y_k=a+(k-1) h, \quad k=1, \dots, M+1.\]

Athugum að hér notum við \(j, k\) sem byrja frá 1 (í staðinn fyrir 0), af því að við höfum í huga að Matlab (eða Octave, eða Mathematica, ...) byrja í 1 í tölusetningu vigra.

Tvívíð tölusetning netpunkta

Hér setjum við \(1\le j \le N+1\) og \(1 \le k \le M+1\), og við tölusetjum netpunktana með \((x_j, y_k)\).

Einföld tölusetning netpunkta

Hér tölusetjum við netpunktana með \((x_i, y_i)\) þar sem \(i= j+(k-1)(N+1)\). Til dæmis setjum við \(k=1\) og skoðum punkta með \(i= j+(k-1)(N+1)=j\), þar sem \(j=1, \dots, N+1\). Síðan veljum við \(k=2\) og skoðum punkta með \(i= j+(k-1)(N+1)=j+(N+1)\), þar sem \(j=1, \dots, N+1\), og svo framvegis.

Uppbygging forrits

Til þess að byggja upp jöfnuhneppi \(A{\mathbf c}={\mathbf b}\) sem nálgar gildi lausna \(u(x_j,y_k)\) á (9), þurfum við líta á eftirfarandi tilvik:

Innri punktar

Skoðum innri punkta \((x_j,y_k)\) þar sem \(1<j<N+1\) og \(1<k<M+1\). Við notum nálgunarjöfnuna (7) hér, og við fáum fylkjastök \(a_{i,i-\ell}, a_{i,i-1}, a_{i,i+1}, a_{i,i+\ell}\) og \(a_{i,i}\), þar sem \(\ell=N+1\). Í hægri hlið hneppisins er \(f_i=f(x_j,y_k)\).

Punktar á jöðrum en ekki hornpunktar

Skoðum punkta á jaðrinum \(\partial D\) sem eru ekki hornpunktar. Ef \(\beta(x_j, y_k)=0\), þá gildir að

\[c_i=\gamma(x_j,y_k)/\alpha(x_j,y_k).\]

Það þýðir að jöfnuhneppið hér er \(a_{i,i}=1\) og í hægri hliðinni \(b_i=\gamma(x_j,y_k)/\alpha(x_j,y_k)\).

Ef \(\beta(x_j,y_k))\neq 0\), þá þurfum við nota nálgunarjöfnuna (7).

Hornpunktar

Ef \(\beta(x_j, y_k)=0\), vitum við eins og áður hvaða gildi fallið \(u\) hefur í punktunum.

Ef \(\beta(x_j,y_k))\neq 0\), þurfum við að fara varlega, af því að föllin \(\alpha\), \(\beta\) og \(\gamma\) geta verið ósamfelld. Gott er að sjá fyrir sér hvað er að gerast í hornpunktinum, og skrifa upp mismunajöfnur.

Gefin gildi í einstaka netpunktum

Ef við viljum (eða vitum) að fallið \(u\) tekur gefið gildi \(U_s\) í einhverjum netpunktum, með \(s=1, \dots, \mu\). Við tölusetjum slíka punkta með \(i\). Þá gildir að einu stök fylkisins \(A\) í línu \(i\) sem eru ekki núll eru \(a_{i,i}=1\). Á hægri hliðinni höfum við \(b_i=U_s\).

Þegar við höfum reiknað út fylkið \(A\) og vigurinn \(b\), þá getum við notað t.d. Matlab, (eða Octave eða Mathematica eða Maple...), til þess að fá nágunargildin \(c_i\). T.d. getum við skrifað í Matlab:

S=sparse(A); c=Sb;

Það er líka gott að teikna graf lausnarinnar. T.d. getum við skrifað í Matlab:

surf(x,y,W’),

og jafnhæðarlínur hennar má teikna með: contour(x,y,W’).